Walkthrough on PCA through the command line
PCA computations through the command line are governed through PCA workflow objects. We describe here how to create and handle them:
Creation of a synthetic data set
dtutorial ttest128 -M 64 -N 64 -linear_tags 1 -tight 1
This generates a set of 128 particles where 64 are slightly closer than the other 64. The particle subtomogram are randomly oriented, but the alignment parameters are known.
Creation of a workflow
Input elements
The input of a PCA workflow are:
- a set of particles (called data container in this article)
- a table that expreses the alignment
- a mask that indicates the area of each alignment particle that will be taken into account during the classification procedure.
Data
dataFolder = 'ttest128/data';
Table
tableFile = 'ttest128/real.tbl';
Mask
We create a cylindrical mask with the dimensions of the particles (40 pixels) mask = dcylinder([20,20],40);
Syntax
We decide a name for the workflow itself, for instance
name = 'classtest128';
Now we are ready to create the workflow:
wb = dpkpca.new(name,'t',tableFile,'d',dataFolder,'m',mask);
This creates an workflow object (arbitrarily called wb in the workspace during the current session). It also creates a folder called classtest128.PCA where results will be stored as they are produced.
Mathematical parameters
The main parameters that can be chosen in this area are:
- bandpass
- symmetry
- binning level (to accelerate the computations)
Computational parameters
The main burden of the PCA computation is the creation of the cross correlation matrix.
Computing device
PCA computations can be run on GPUs of on CPUs, in both cases in parallel.
Size of parallel blocks
The
Running
In this workflow we run the steps one by one to discuss them. In real workflows, you can use the run methods to just launch all steps sequentially.
Prealigning
wb.steps.items.prealign.compute();
Correlation matrix
All pairs of correlations are computed in blocks, as described above
wb.steps.items.ccmatrix.compute();
Eigentable
The correlation matrix is diagonalised. The eigenvectors are used to expressed as the particles as combinations of weights.
wb.steps.items.eigentable.compute();
These weights are ordered in descending order relative to their impact on the variance of the set, ideally a particle should be represented by its few components on this basis. The weights are stored in a regula Dynamo table. First eigencomponent of a particle goes into column 41.
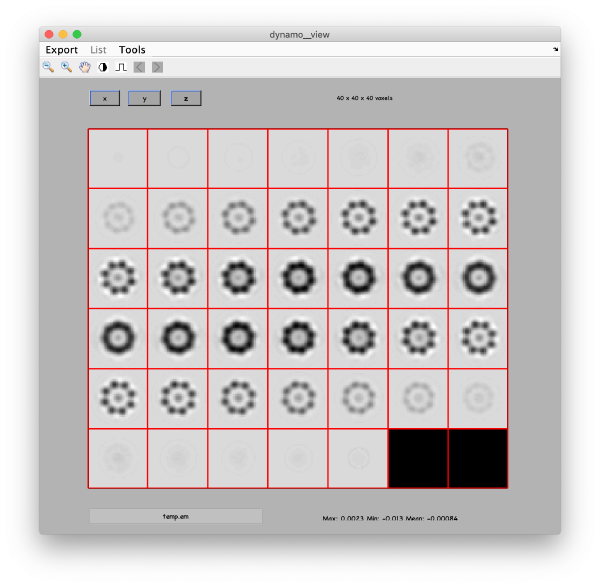
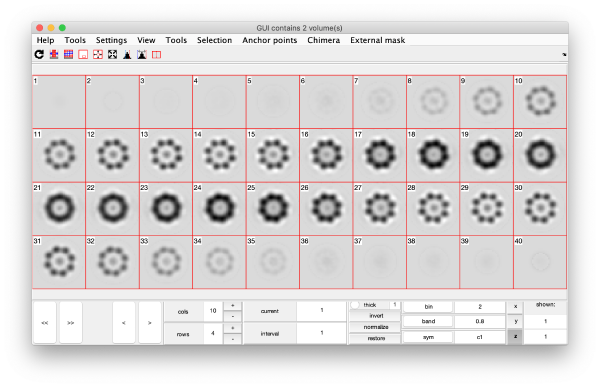
Eigenvolumes
The eigenvectors are expressed as three=dimensional volumes.
wb.steps.items.eigenvolumes.compute();
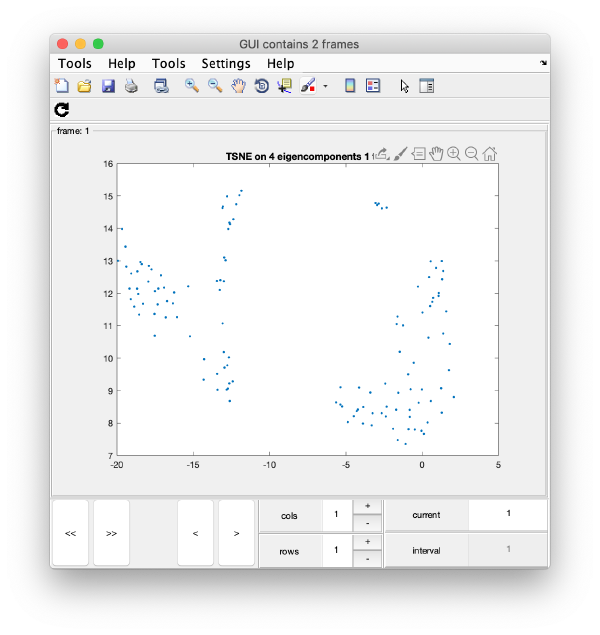
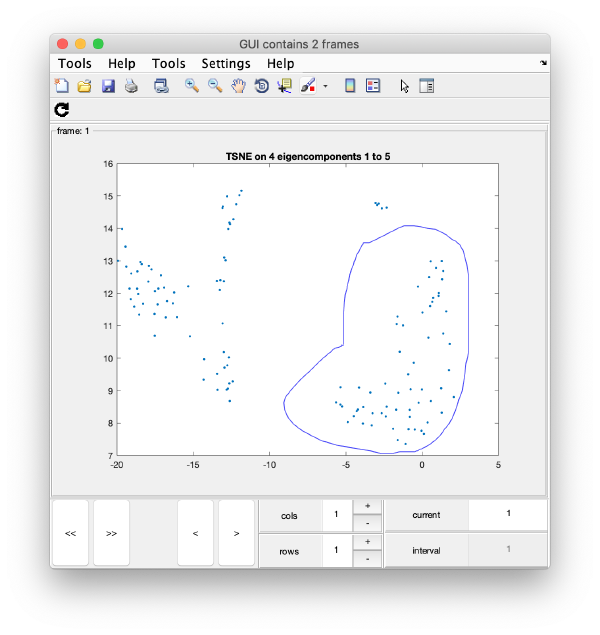
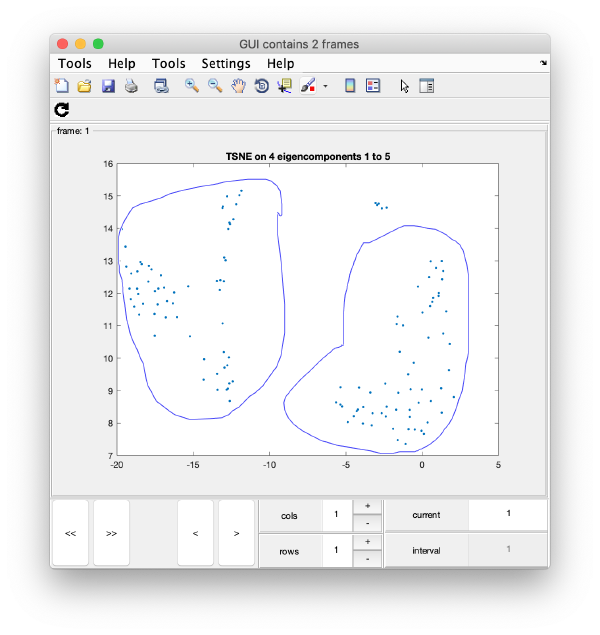
TSNE reduction
TSNE remaps the particles into 2D maps which can be visualised and operated interactively.
wb.steps.items.tsene.compute();
Visualization
Computed elements have been stored in the workflow folder. Some of them () can be directly access through workflow tools.
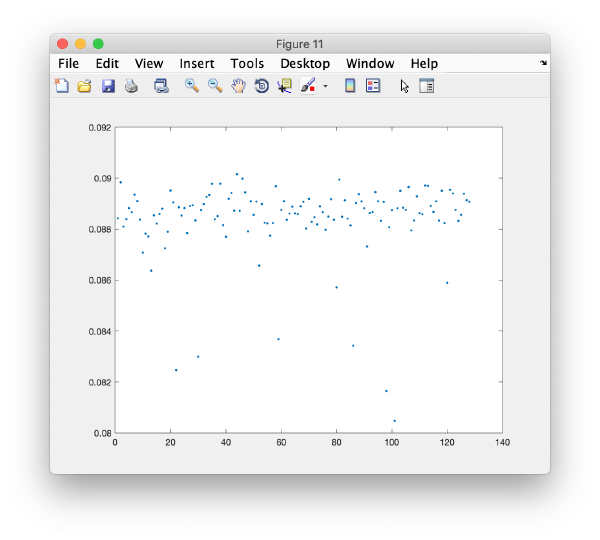
Correlation matrix
m=wb.getCCMatrix();
figure;dshow(cmm);h=gca();h.YDir = 'reverse';
Eigencomponents
Series of plots
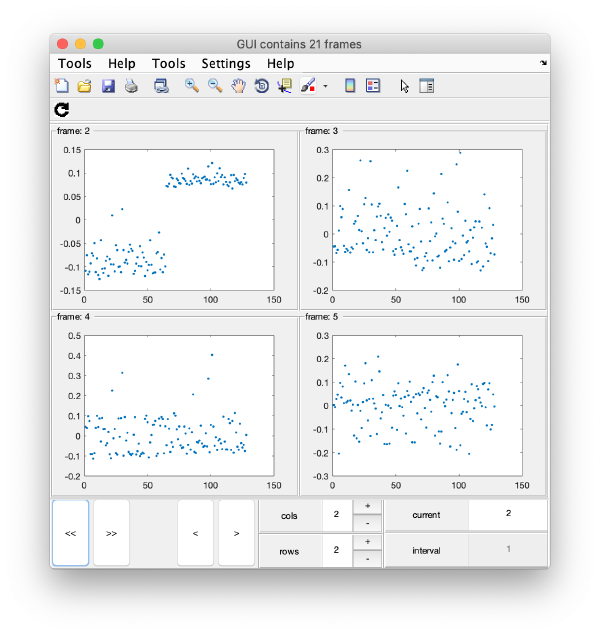
To check all the eigencomponents, it is a good idea to do some scripting. The script below uses a handy Dynamo trick to create several plots in the same figure.
gui = mbgraph.montage();
for i=1:10
plot(m(:,i),'.','Parent',gui.gca);
% gui.gca captures the
gui.step;
end
gui.first();
gui.shg();
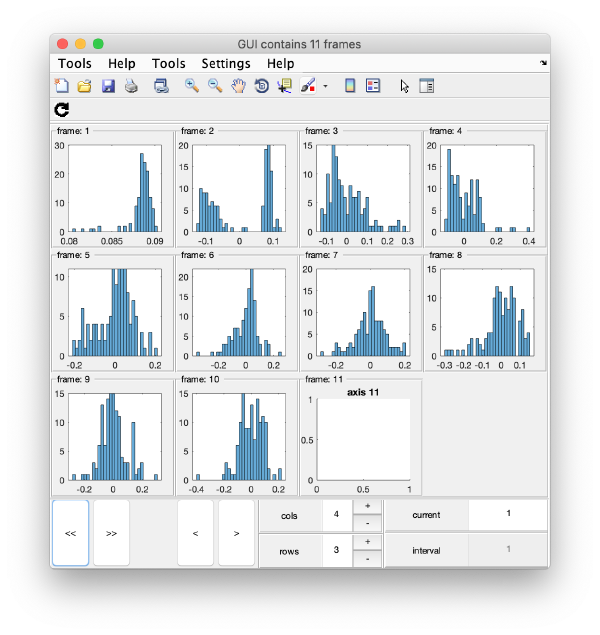
Series of histograms
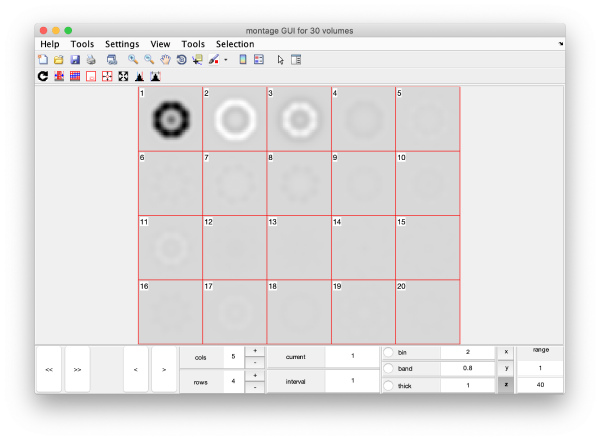
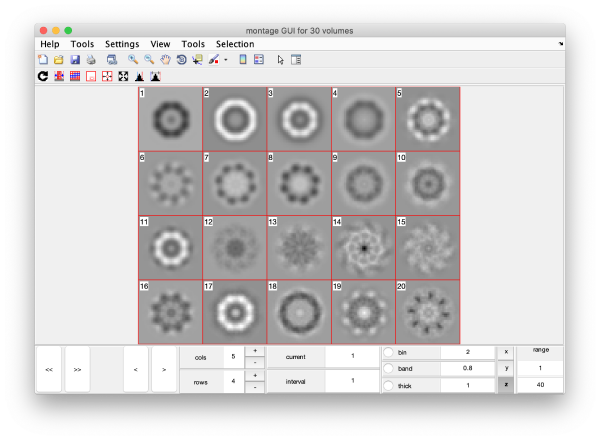
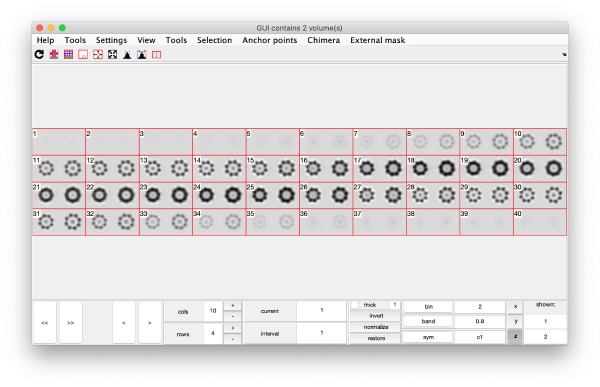
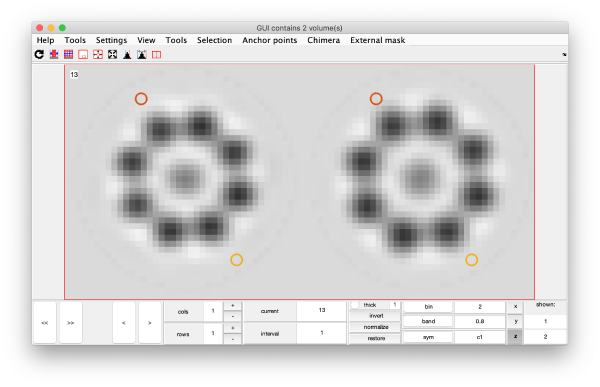
Eigenvolumes
eigSet=wb.getEigenvolume(1:30);
mbvol.groups.montage(eigSet);
mbvol.groups.montage(dynamo_normalize_roi(eigSet));
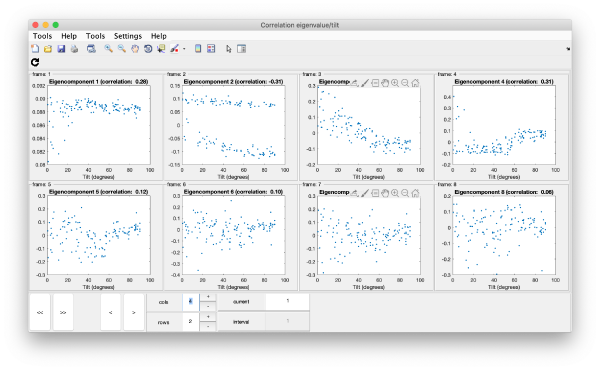
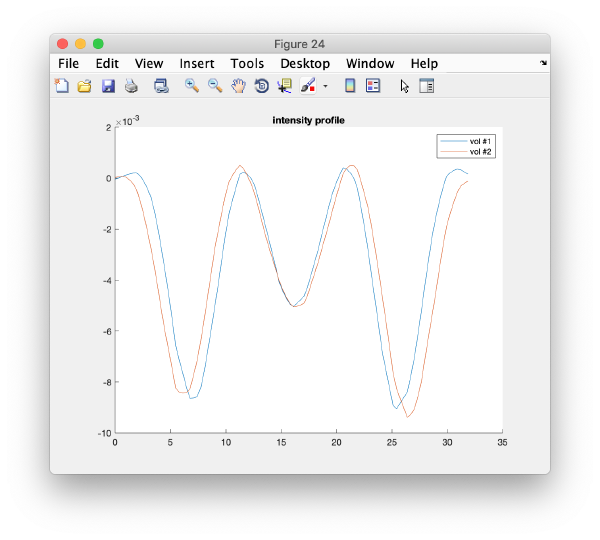
Correlation of tilts
It is a good idea to check if some eigenvolumes correlate strongly with the tilt.
wb.show.correlationEigenvectorTilt(1:10)
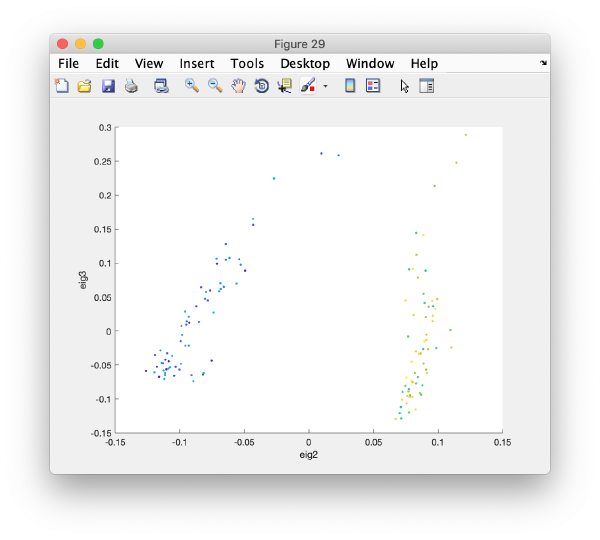
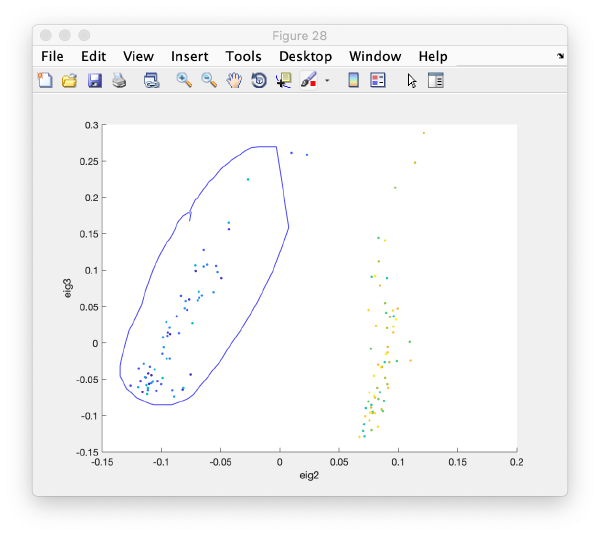
In this plot, each point represents a particle in your data set. We see that in this particular experiment, eigencomponent 3 seems to have been "corrupted by the missing wedge"