Vesicle models

Vesicle models are appropriate when particles are evenly distributed on surfaces reasonably similar to spheres or ellipsoids. The model can estimate the center and radius provided points provided by the user in the visible part of the object, or the other way round, letting the user provided center and radius.

Important parameters

Radius

Given in pixels. Can be estimated or provided by the user.

Center

Given in pixels. Can be estimated or provided by the user.

Separation

Given in pixels. Defines the mean separation of the cropping positions to be defined in the vesicle surface. When choosing this value, you should think on oversampling the actual distribution of particles that you expect.

Picking vesicles in a tomogram browser

There are different methods for vesicle picking interactively.

Cloud of points

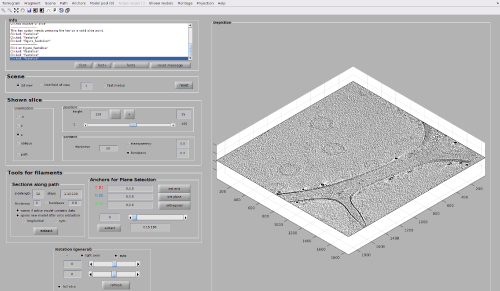
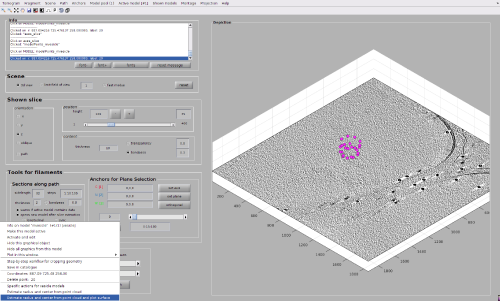
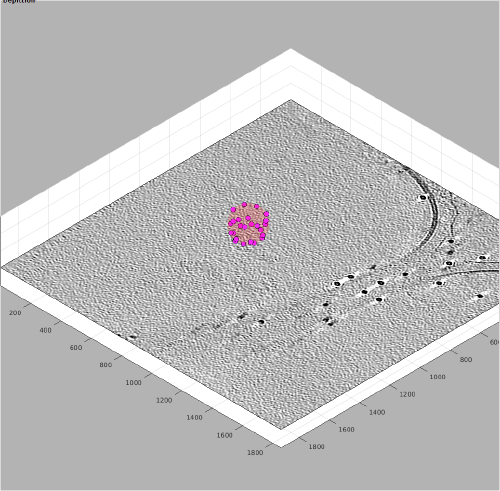
The most robust method requires from the user to pick several points in each vesicle model, and then let Dynamo fit the radius and the center. This procedure can be performed through the browser dtmslice, as shown in the next images.

A tomogram with several vesicles shown in dtmslice

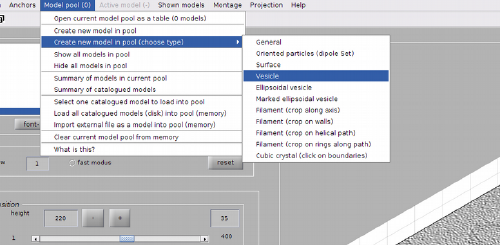
First of all we need to define a model of type vesicle into the model pool viewed by dtmslice.

Creation of a vesicle model

Once the model is created an active, we can navigate in the tomogram (for instance, by dragging the slice through movement of the cursor while the main mouse button is pressed). Three layers are normally enough.

Click vesicle points (in pink) on different z levels (use [c] to pick each)

After collecting four of five points on each layer, we can zoom out (with, for instance, [-] ) and bring the slice to a slower z value.

View from a lower z level

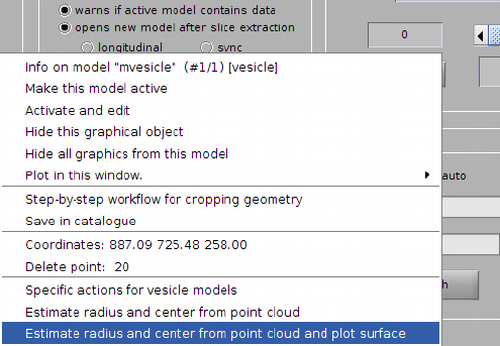
Now, we just need to invoke the method that fits the center and radius properties of a vesicle given a cloud of points. From the command line, this method is called approximateGeometryFromPoints. In the browser dtmslice we can invoke it directly by secondary clicking on one of the points of the model and selecting the option for fitting and plotting.

Menu options after secondary click on a model point

Detailed view on the menu options.

A transparent surface should be visible, allowing you to judge the quality of the fitting quickly sliding the slice up and down.

Depiction of the fitted vesicle surface

From dipole det models

It is also possible to use other models to define vesicle models. This is useful when you have several vesicles in one tomogram, and you don't want to initiate a vesicle model for each one of them. The dipole set model allows creating in a single model several 'dipoles', each one of them having a center, a north and a south. We can use this model to define each vesicle from a dipole: the center property of the dipole can be directly transferred to the vesicle, and the radius of the vesicle can be defined as the distance between the center and north coordinates registered in the dipole.

You can use this code to convert a dipole set into a set of vesicle models. The code assume that the dipoles set model is in the catalogue, and that the resulting models are also saved into the catalogue.

% 
dipoleSetModelFile = '~/first/tomograms/volume_1/models/dipoleset.omd'; % absolute path to your model

% reads the model
ds = dread(dipoleSetModelFile);

% checks the number of individual dipoles
disp(sprintf('Found %d dipoles in the set',length(ds.dipoles)));

% loops on all the dipoles present in the set
for i=1:length(ds.dipoles);
    
    % selects the i-th individual dipole in the set
    dipole = ds.dipoles{i};
       
    % creates a vesicle model   
    v = dmodels.vesicle();

    % prepares a name for each individual dipole
    v.name = sprintf('%srawVesicle_%d',ds.name,i);
   
    % links the created model with the catalogued volume 
    % of the dipole set module
    v.cvolume = ds.cvolume;
    
    % initiates the vesicle model
    v.center = dipole.center;
    v.radius = norm(dipole.center - dipole.north);
    
    % saves the model back into the catalogue
    v.saveInCatalogue();
     
end

Command line

Here come some examples of creation and manipulation of vesicle models from the command line

Given center and radius

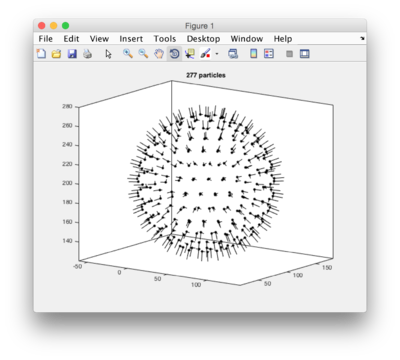
a = dmodels.vesicle(); % creates an empty vesicle model
a.radius = 70;
a.center = [40,100,200];
a.separation = 15;
a.updateCrop();  % here it will some time computing the particles.
t=a.grepTable(); % extracts the table
dtplot(t,'profile','oriented_positions'); % scatter plot of images
axis equal; % for a better visualization, same scale an x,y,z
shg

Table plot of positions and particles generated by a vesicle model