Difference between revisions of "Walkthrough for template matching"
| Line 83: | Line 83: | ||
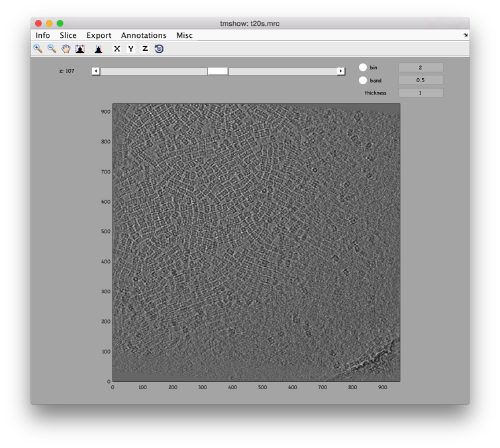
[[ File:TemplateMatchingTomoslicePickTop.png |thumb|center|500px| Use the wheel to go up and down in the tomogram to locate top views ]] | [[ File:TemplateMatchingTomoslicePickTop.png |thumb|center|500px| Use the wheel to go up and down in the tomogram to locate top views ]] | ||
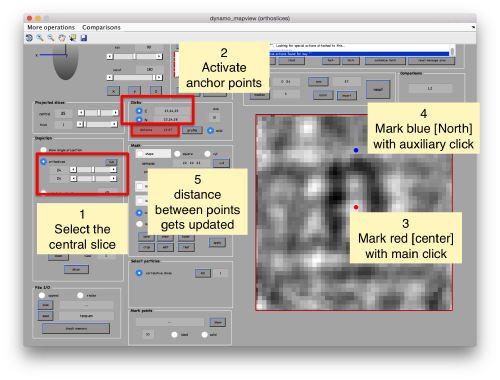
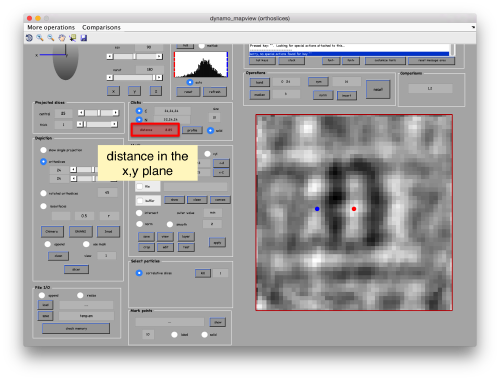
| − | When you have clicked around ten, we will prepare to crop them out of the tomogram. For this, we need to get | + | When you have clicked around ten, we will prepare to crop them out of the tomogram. For this, we first need to get an approximative idea of how big should be the box. With the keys [1] and [2] you can place anchor points in the scene. Auxiliary click in the bar between them shows the distance (in pixels of the unbinned tomogram). In view of the measured distance of around 32, we will use a cropping box size of 48 pixels, in order to ensure that the particles will comfortably fit inside the boxes, as our clicks will not be very precise. |
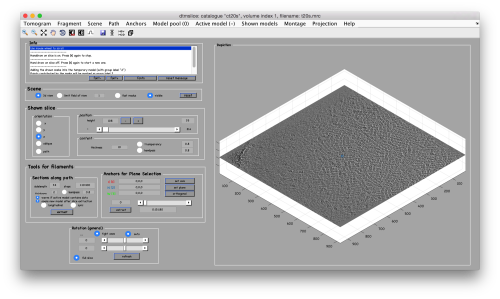
[[ File:TemplateMatchingMeasure.png |thumb|center|500px| Measure distances with the [1] and [2] anchors ]] | [[ File:TemplateMatchingMeasure.png |thumb|center|500px| Measure distances with the [1] and [2] anchors ]] | ||
Revision as of 12:24, 25 November 2017
Dynamo includes a set of tools for location of particles inside tomograms. The most simple one is template matching.
Contents
Template matching
In this technique, a template representing a molecule of interest is systematically cross-correlated against a tomogram, producing a cross-correlation map of the tomogram. Each pixel in this map represents a score assigned the corresponding pixel in the tomogram map. This score measures the similarity of the neighbourhood of the tomogram pixel to the used template. This similarity is measured exclusively inside a mask.
Data set
Tomogram description
The tomogram contains a buffer with T20S proteasome on a holey carbon grid collected on a Krios + K2. Original pixelsize was 1.76 angstroms. The tomogram provided here has bin binned twice (yielding thus 7.04 ang), defocus is 4.4 microns, no CTF correction, no energy filter.
Acknowledgements
The tomogram has been kindly provided by Alex Noble, from the New York Structural Biology Center. Data collection was performed using Leginon and Appion-Protomo at the Simons Electron Microscopy Center and National Resource for Automated Molecular Microscopy located at the New York Structural Biology Center, supported by grants from the Simons Foundation (349247), NYSTAR, and the NIH National Institute of General Medical Sciences (GM103310) with additional support from Agouron Institute [Grant Number: F00316].
Getting the tomogram
In Linux, you can write:
wget https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/t20s/t20s.mrc
the corresponding command is curl -O in the Mac.
Visualizing the tomogram
We can get a first glance on how the tomogram looks like:
dtmshow -otf t20s.mrc
to use the on-the-fly access to the slice shown at each given moment, or
v = dread('t20s.mrc');dtmshow(v);
to preload the full tomogram into a memory variable (arbitrarily called v). In either option, you will see, the proteasomes are densely packed in an layer. The layer is slightly oblique, what can be seen browsing through z or y.
Navigating on-the-fly you'll see that transitions in y are slower than transitions in z, because all the pixels of the same slice are stored sequentially in the disk.
Estimation of the missing wedge
We can quickly check the extent of the missing wedge in the tomogram. We extract a sample of the tomogram:
fragment = dynamo_read_subtomogram('t20s.mrc', 'r',64,'c',[450,450,100]);
and plot a map of the distribution of the Fourier coefficients:
dynamo_wedge_estimate(fragment,'show',1);
Creating a template
There are different strategies to create the first template. In the case where the general shape of each protein is roughly recognisable by eye, it is not difficult to just crop and align manually some of the particles. When this is not possible, you have the option of using a density map that mimics the general topology of your protein.
Through manual alignment
We will use a model inside tmslice to pick a set of ~10 particles. We will then crop them, and align them manually using dgallery
Manual selection of some particles
We use for this our tool dtmslice. As the tomogram is provided is fairly small you can probably just open it without any further binning.
dtmslice t20s.mrc -c ct20s
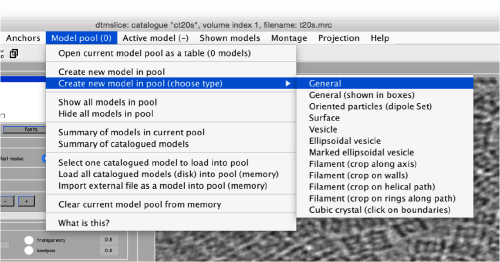
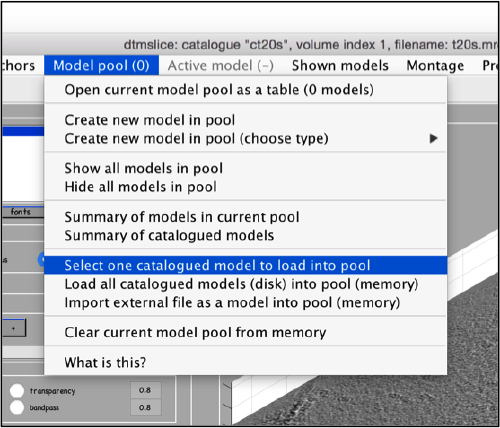
Use the model pool menu to add a new model of type General
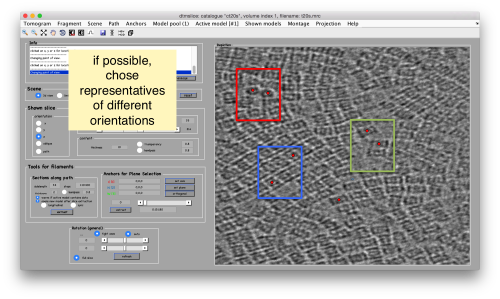
Try to pick particles on different orientations, both in top and side views. Particles are picked with the key C, use backspace to clear the latest selection.
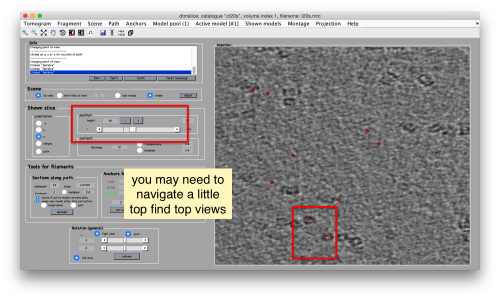
You can move the slice with the z slidebar in the control panel, or dragging it while the mouse button is pressed. Top views are more abundant below the crowded accumulation of side views in the central slice.
When you have clicked around ten, we will prepare to crop them out of the tomogram. For this, we first need to get an approximative idea of how big should be the box. With the keys [1] and [2] you can place anchor points in the scene. Auxiliary click in the bar between them shows the distance (in pixels of the unbinned tomogram). In view of the measured distance of around 32, we will use a cropping box size of 48 pixels, in order to ensure that the particles will comfortably fit inside the boxes, as our clicks will not be very precise.
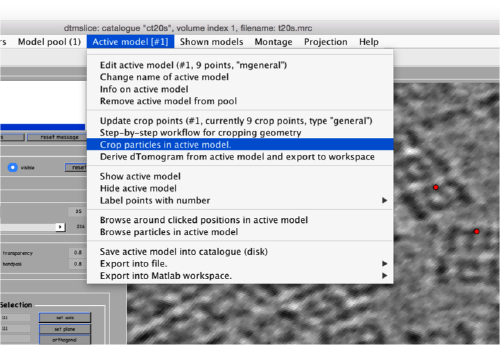
Now we can open the dtcrop utility for this model, by visiting the Active model" menu.
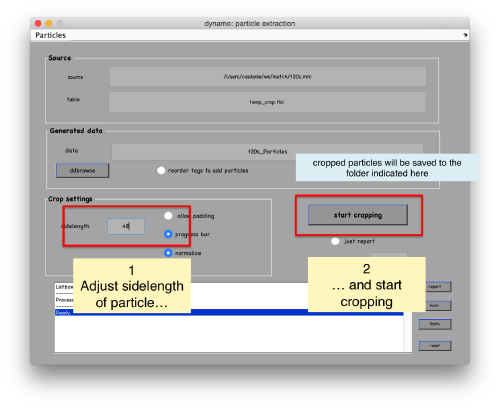
In the GUI that pops up we can fix the sidelength to the value 48.
After completion of the cropping process, you will get a data folder called t20s_Particles, which will also contain a table file called t20s_Particles/crop.tbl
Manual alignment of some particles
Now we want to align the particles. We open them inside the dgallery browser:
dgallery -d t20s_Particles -t t20s_particles/crop.tbl
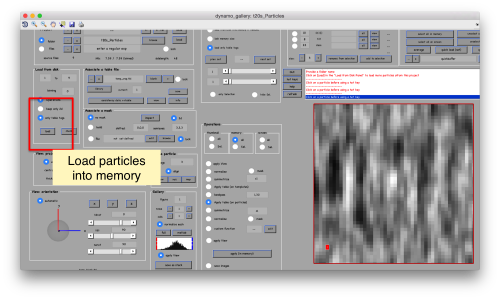
This GUI has several functionalities. We will focus in using it to quickly get an alignment of the particles. For this, we first load the particles expressed in the table into the internal memory of the gallery by clicking into Load.
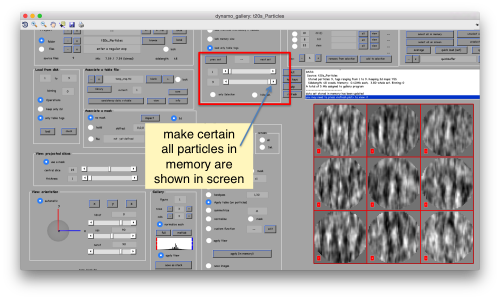
This seems not to have any effect in the depiction: you need to fix the range of the depicted particles moving the slider bar. When you do so, each particle will appear in the scene as a single red box.
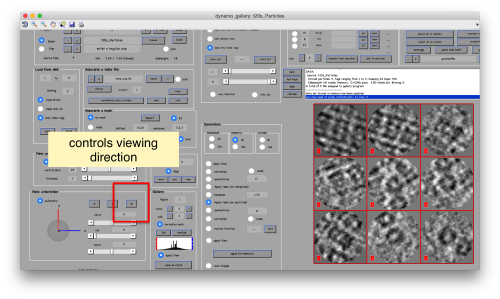
You can play with different settings for viewing, like the direction (x, y or z)
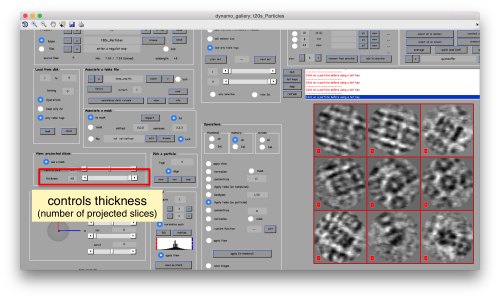
or the number of slices that are projected into the depicted image for each particle.
Then, you go through each particle and indicate a point that you considere that could lay in the central axis of the particle by clicking on [N]. The particle will rotate on screen to match this direction. The center of the particle can also be set by clicking on [C]. In this case, the particle will not rotate, but will shift to put its center on the spot where the click was operated.
Top views viewed along z should not be changed with the N click, only with the C to recenter them if necessary.
You may need to complete two rounds of operating on the particles, changing the viewing direction (first in x, then in y)
Averaging manually aligned particles
We export the table we have computed
Now we can use the table (saved as file quickbuffer.tbl by default) to create an average of the manually aligned particles:
oa = daverage('t20s_Particles','t','quickbuffer.tbl');
which can be visualized in mapview
dmapview(oa);
Creating a tight mask
Measure distances
Open the computed average in mapview,
dmapview(oa.average);
set the view to the XZ or YZ planes,
Connect the anchors [C] and [N] (which in mapview are placed simply with the main and the auxiliar click), and measure the semiaxis of the average. Here, we want to click well outside of the signal, as we are measuring the distances that define a mask that needs to contain the average.
Now, move the [N] anchor to move the radius of the average in the xy plane,
Create mask
We now symmetrize the density map. Use an arbitrary high value, we have use 17 in our example. The goal is simply to have a strong representation of the signal and to check how the template fits inside the mask that we will create later.
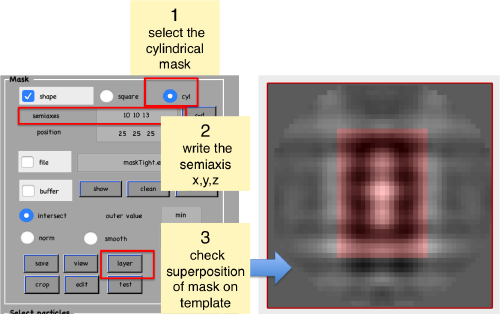
Now, we create a cylindrical mask using the lengths of the semiaxes that we have measured using the anchor points.
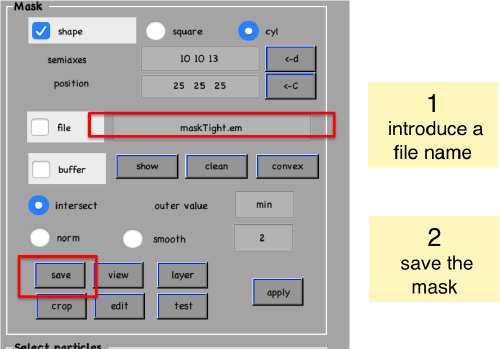
We save the created mask into a file
Cropping the borders of a template
We check how the mask looks like on the template
shifted =circshift(dsym(oa.average,'c17'),[0,0,-1]);dslices(shifted,'y','overlay','maskTight.em','overlay_as','mask');
The circshift operation is just shifting the template, as it seems that it is not well centered. It's normal: it's difficult to catch a perfect centering in a manual alignment. Probably in your own data set things will look slightly different. If necessary, you should try with different parameters, and stick with the one that looks like the best alignment. Then save it into a variable in the memory space:
shifted = circshift(dsym(oa.average,'c17'),[0,0,-1]);
Now we can extract the part of the created template where we actually have signal:
cropped = dynamo_crop(shifted ,32);
We create a file to contain this cropped template:
dwrite(cropped,'average32.em');
and proceed similarly with the mask:
dwrite(dcrop(dread('maskTight.em'),32),'maskTight32.em');
Through geometrical shapes
Alternatively, you can use dynamo_mask or dynamo_tube to create a synthetic model.
Creating a template matching process
The main function is dynamo_match
pts = dynamo_match('t20s.mrc','average32.em','mask','maskTight32.em',....
'outputFolder','cs30',...
'ytilt',[-39,36],'sc',[256,256,256],'cr',360,'cs',30,'bin',1);
- 'bin'
allows binning on the fly. Template, mask and tomograms are input in original size. - 'sc' : size of chunk
This is the maximum extent of a block in the unbinned tomogram that will be kept in memory by each one of the processors working in parallel (only one in this experiment). We need to be careful not to crowd the available memory. - 'cr' : cone range
orientations will be looked for inside a cone. In this context, the most usual values are 360 (sample the full sphere) or 0 (do not scan orientations) - 'cs' : cone sampling
Determines the scanning density inside the sphere.
You should get the following response on the screen (will take around 5 minutes to complete)
------------------------------------------------------------
Template matching process.
computing in CPU
Output folder: cs30.TM
A total of 1 tiles have been created
- Mb per tile (reading) : 724.19
- Mb per tile (operation) : 663.84
... initializing output elements
Preparing to run on 25 blocks
Running on single processor
Computing tile 1
<Information for each block>
... tile 1 finished in 387 seconds (8 for setup; 7.73 per triplet)
[ok] ... template matching process completed upto creation of cross correlation
you can proceed to peak location and particle extraction.
------------------------------------------------------------
The main result of dynamo_match is a volume (cross correlation volume) that assigns a score to each pixel. This tomogram is written in the file cs30/CC.mrc. Some auxiliary outputs are other volumes that store the angles [tdrot,tilt,narot] that maximize the cross-correlation for each pixel in the volume. It also creates a binned version of the tomogram, which will be useful to quickly crop particles for the purpose of evaluating the quality of the template matching.
The Process object
The return pts of the function dynamo_match is an object that keeps track of the location of all the created output, and is used in the subsequent steps that extract the actual location of the peaks
Locating cross correlation peaks
Now we need to identify which peaks of the cross correlation correspond to actual particles.
Looking at the cross correlation map
We first examine the cross correlation map.
pts.showCC
It is possible to operate on the map (through bandpassing or gaussian filtering) to smoothen the volume and get rid of many spurious peaks, but we won't do it like thtr in this exercise.
Looking at the cross correlation profile
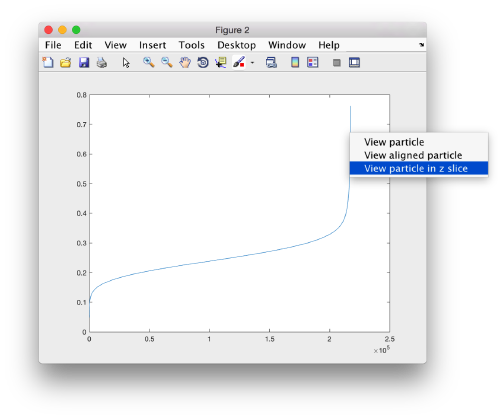
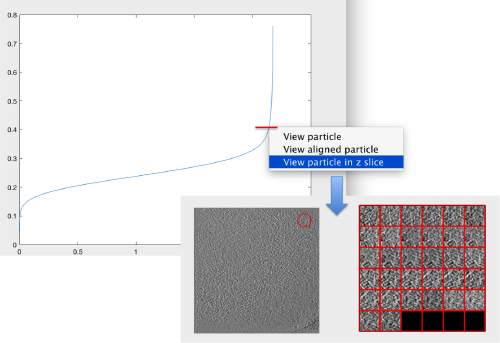
We can get a plot of the cross-correlation value found on the local maxima of the cc volume wiith the order
pts.peaks.plotCCPeaks('sidelength',32)
The cross-correlation values of the peaks appear in ascending order. We can check the quality of the peaks by auxiliary clicking on the curve to select one particle and then selecting some visualization option.
The sidelength that we pass will be used for this visualization options to crop the particle around the peak.
We click on a couple of particles in the area of kink in the cross-correlation to roughly estimate the cross-correlation threshold. In out case, it seems to be around 0.37 (being rather conservative)
In the gaussian distribution below this ara , the peaks do not correspond to particles
Extracting a table
A table can be extracted through:
myTable = pts.peaks.computeTable('mcc',0.38);
In this procedure, the template is first placed back in the position of highest correlation, using the alignment parameters. Then the next correlation maximum is considered, and the template is placed in its location. If the second placement overlaps with the previous one, the second one is considered an spurious maximum and skipped. This procedure is repeated till a threshold of cross correlation is attained (0.38 in this case).
This order creates the variable myTable in the workspace, and stores a copy of it inside the pts objects, so that we can use it to invoke some axiliary functions to evaluate the result of our experiment.
Visual evaluation of results
Looking at table positions
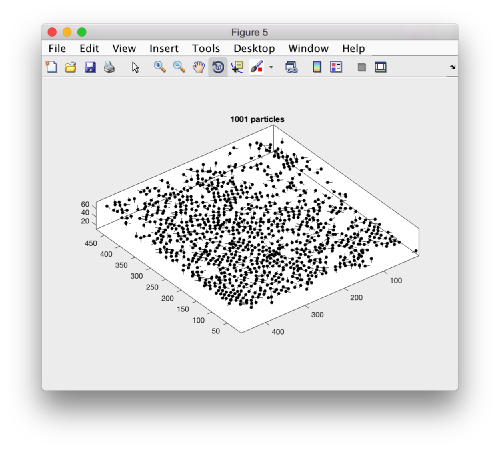
A sketch of the 3d positions of the particles can be created through
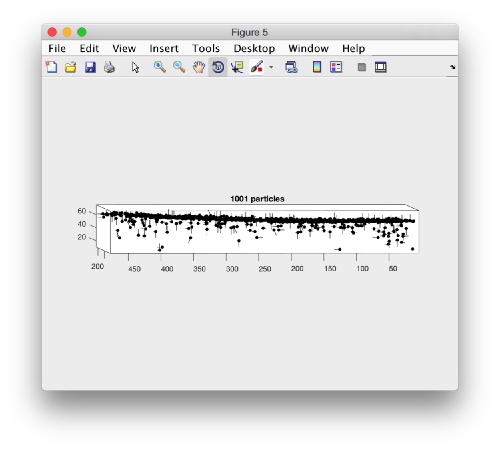
dtplot(myTable,'pf','oriented_positions');
where 'pf' stands for profile. There are different predefined visualization profiles that can be passed to dtplot
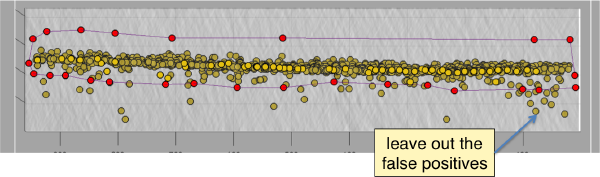
When rotated to show the YZ plane we see the shape of the layer were proteosomes are packing. This indicates that we don't have too many false positives.
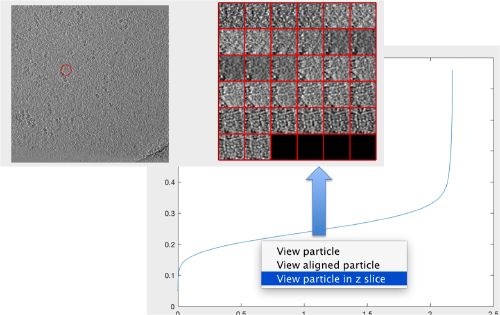
Looking at cropped particles
We can check how the individual particles look like on a gallery modus:
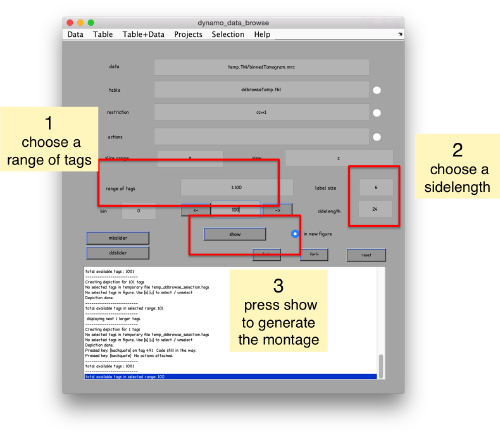
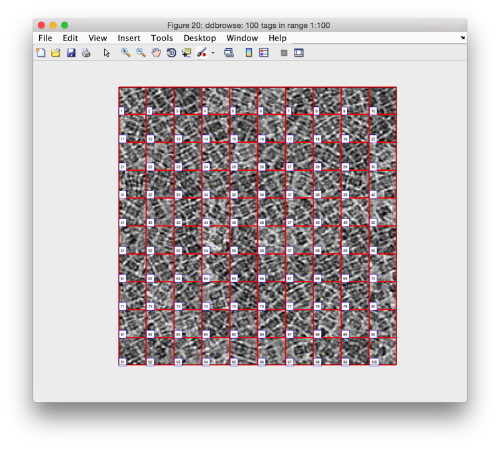
pts.peaks.browse();
This order just opens ddbrowse. We are using here the support object peaks, but this command is equivalent to just invoking ddbrowse as
ddbrowse('d','cs30.TM/tomogramBinned.mrc','t',myTable);
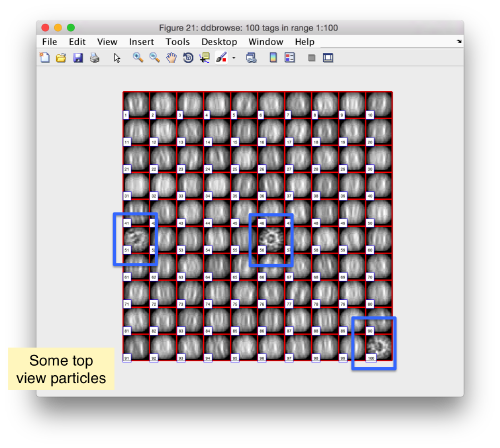
We check the first 100 particles, as they appear inside the tomogram (i.e., without aligning them). We use the z direction (corresponding to the direction of the electron beam)
Now we look at them along the z direction of the aligned particles.
Along the z direction we can only recognize particles that were already in a top view/
Note the different appearance of the particles along the x and y direction.
This different behaviour occurs because we haven't used any rotational search during the template matching procedure. Thus, the azimuthal angle is initialized to zero, creating this bias.
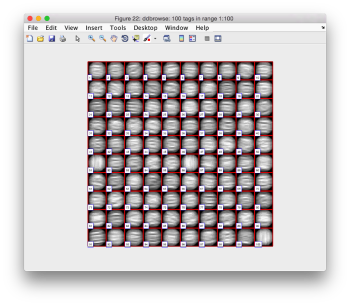
Looking at averages
The bias visualized in the aligned particles is not important for the purpose of locating the particles, but we need to take it into account if we want to produce a new template on the results we just computed. A simple averaging
oap = pts.peaks.average(48);
will produce a density map showing this different behaviour along x and y. Note that we need to introduce a sidelength (48), as the particles have never been cropped to this point, we are extracting them continuously from the binned tomogram.
dview(oap);
We should randomize the azimuthal angle
oapRandomized = pts.peaks.average(48,'ra',1);
in order to get a well balanced template
Getting the tables back into the catalogue
You don't need to operate with the catalogue: you could just use dtcrop on the just computed table to extract particles from the original tomogram into a data folder. However, cataloguing has to advantages:
- Eases keeping track of all the steps you've performed, specially if you are going to use several tomograms, and..
- allows you to visualize the peaks on the tomogram interactively, so that you can delete false positives or add peaks that were not located by the template matching.
Rescaling the table
Remember that the table that we are working with has the scale of the auxiliary binned volume that has been created along with the CC matrix. In the catalogue, we want to work with the particles in their original scale.
tableOriginalScale = dynamo_table_rescale(myTable,'factor',2);
In the syntax of dynamo_table_rescale, the factor is expressed in terms of how many times is the apix in the original table bigger than in the target table to be computed. In our case, the target table was computed with an apix of 14 Angstrom (one time binned in relation to the tomogram t20s.rec, with an apix of 7.04A). The factor is thus 2. In case of doubt, it is convenient to just run
dtinfo(tableOriginalScale);
to check the extent of the entries in the columns 24, 25 and 26, which are positions (in pixels) of the particles indexed by the table. Now, if we write the upscaled table into a file
dwrite(tableOriginalScale,'peaks.tbl');
Entering result in catalogue
we can just put this table back into the catalogue through:
dmimport -t peaks.tbl -c ct20s -i 1 -mn ccpeaks
which will create a model called ccpeaks and assign it to the first volume (-i 1) in the catalogue ct20s. You can check it by writing:
dcm -c ct20s -i 1 -l m
which asks for a listing of models (-l m) in the first volume of the catalogue.
The model is editable and you can add or remove individual points.
Discarding regions
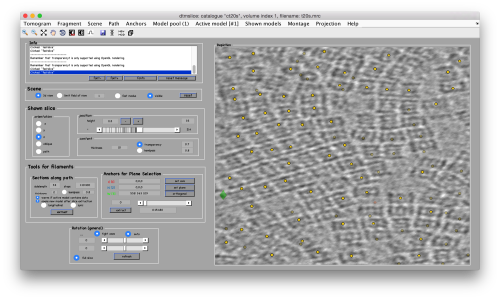
Below the planar area that contains the most proteosomes, we see several false positives. Some false positives insist in having high correlation peaks and cannot be discarded by thresholding. In order to remove them, we can inspect and remove them individually. If they are too many, we will probably prefer to mark regions in the tomogram where we want to keep of discard peaks. In this case we will mark a polygon in the XZ plane, and keep those peaks that fall inside (indepently of the y coordinate).
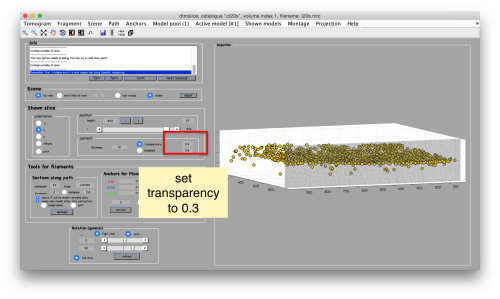
To to this, press [Y] to get a slice orthogonal to this direction, and adjust the transparence in order to see the points behind the slice.
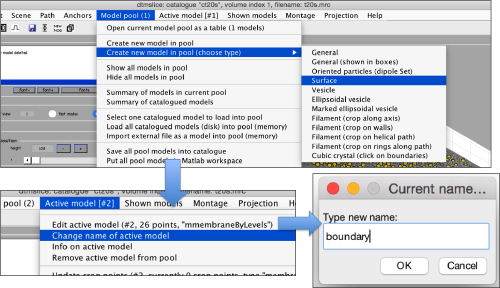
Now, we create a surface model, and change its name to boundary for future reference.
Use the mouse while keeping CTRL pressed to adjust the view and see along the direction. Then, use C to draw a line that enclose the area where we see valid peaks.
Don't forget to save the model when you are done.
Keeping peaks inside the selected polygon
Now, we can read both models into memory
dcmodels ct20s -nc peaks -ws output
p = dread(output.files{1});
dcmodels ct20s -nc bound -ws output
b = dread(output.files{1});
Consider only the XZ coordinates in both
pXZ = p.points(:,[1,3]); bXZ = b.points(:,[1,3]);
and compute the indices of the points in the peaks model that are enclosed inside the boundary model (in the xz plane).
indicesOfPInsideB = inpolygon(pXZ(:,1),pXZ(:,2),bXZ(:,1),bXZ(:,2));
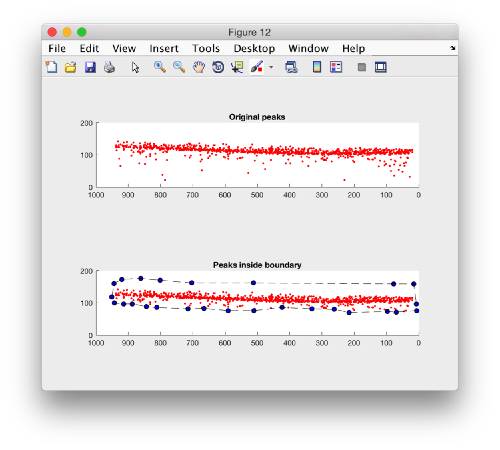
Plotting the kept peaks
f = figure();
hs1 = subplot(2,1,1);
h = dpkgeom.plotCloud(p.points); axis equal
h.Marker = '.';
view([0,1,0]);
hs1.ZLim = [0,200];
hs1.XLim = [0,1000];
title('Original peaks');
hs2 = subplot(2,1,2);
h = dpkgeom.plotCloud(p.points(indicesOfPInsideB,:)); axis equal;
h.Marker = '.';
hold on;
hB = dpkgeom.plotCloud(b.points); axis equal
hB.Marker = 'o';
hB.LineStyle = '--';
hB.MarkerFaceColor = 'b';
hB.Color = 'k';
title('Peaks inside boundary');
view([0,1,0]);
axis(hs2,axis(hs1));