Difference between revisions of "Advanced starters guide"
| Line 7: | Line 7: | ||
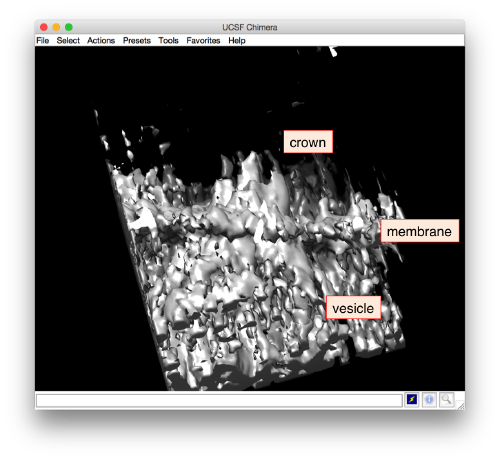
The data is a fraction of a tomogram. The full tomogram was used in "Cryo-electron tomography reveals novel features of a viral RNA replication compartment." (Ertel et al.), and represents several FHV viruses docked in the membrane of a mithocondrion. | The data is a fraction of a tomogram. The full tomogram was used in "Cryo-electron tomography reveals novel features of a viral RNA replication compartment." (Ertel et al.), and represents several FHV viruses docked in the membrane of a mithocondrion. | ||
| + | [[File:FhvDefinitionCrown|thumb|center|500px|Average with hundreds of particles. The "crown" area in red ]] | ||
== Downloading == | == Downloading == | ||
Revision as of 17:49, 17 July 2017
This walkthrough uses a small size example based on a real tomogram to covers several tasks.
Contents
- 1 The example data set
- 2 Downloading
- 3 Cataloguing the tomogram
- 4 Annotation of particle positions
- 5 Cropping particles
- 6 Project to find membrane orientations
- 7 Aligning the axis of symmetry
- 8 Project for rotational alignment
- 9 Project with rotational randomization
- 10 Project for localized alignment
The example data set
The data is a fraction of a tomogram. The full tomogram was used in "Cryo-electron tomography reveals novel features of a viral RNA replication compartment." (Ertel et al.), and represents several FHV viruses docked in the membrane of a mithocondrion.
Downloading
In principle, you can download all the files related to this example with the command:
dpkhelp.wiki.downloadExample('fhv');
If it fails under Matlab or the Dynamo command line, you can try to directly use the linux order
wget https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/fhv/crop.rec
or
curl -O https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/fhv/crop.rec
unter MacOS.
This should have created the file called crop.rec in your current directory.
Size check of a file
You're probably curious to see what's inside, so that let's write first:
dfile crop.rec
to let Dynamo check the dimensions of the file. The header of a .rec file is readed as a regular mrc, yielding:
filetype: volume size: 1285 x 956 x 786
So, it's a tomogram.
Lightweight visualization
We can inspect quickly its contents with dtmshow
dtmshow -otf crop.rec
Hereby, the flag -otf means "on the fly", telling dtmshow to not preload the full tomogram, but to access in disk the individual slices that are needed when inspecting a particular area.
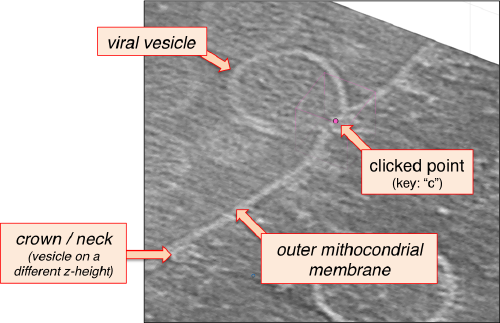
Go up and down. We want to select the locations were the vesicles intersect the mithocondrion membrane and average them together. For this, we need to catalogue the tomogram, so that our annotations are stored with a clear relationship with the tomogram.
Cataloguing the tomogram
We can create catalogues just to contain a single tomogram. They are useful to keep track of all annotations, and of the typical transforms (binning, cropping of fractions) that we usually perform on a larged size tomogram of interest. In this case, we can create the catalogue directly from the command line:
>dcm -create fhv
where dcm is the short form of dynamo_catalogue_manager and fhv is just an arbitrary name. The just created catalogue is empty, and we can add our tomogram with:
dcm -c fhv -at crop.rec
We can check that the tomogram is in the catalogue by asking Dynamo to show the contents of the catalogue
dcm -c fhv -l tomograms
or
dcm -c fhv -l t
The flag -l asks Dynamo to list items of a given category of catalogue contents, in this case tomograms
Prebinning the tomograms
We typically want to prebin the tomogram, i.e., have a version of smaller size that is known to the catalogue. This version will be useful in some operations that require a full tomogram in memory, an operation that can consume much memory and need a long time. In this example, this is probably not necessary: a tomogram with a sidelength on x and y of ~1000 pixels shouldn't pose any visualization problem. Still, in the command line, we can write
dynamo_catalogue_bin('fhv', 1, 'zchunk', 300);
where the parameter zchunk represents the maximum number of z slices that are kept simultaneously in the memory during the binning process. This parameter might be important for larger size tomograms.
Operation with GUI
These steps could have been performed thorugh the dcm GUI <tbi>
Annotation of particle positions
Now we can open the tomogram through the catalogue:
dtmslice crop.rec -c fhv -prebinned 1
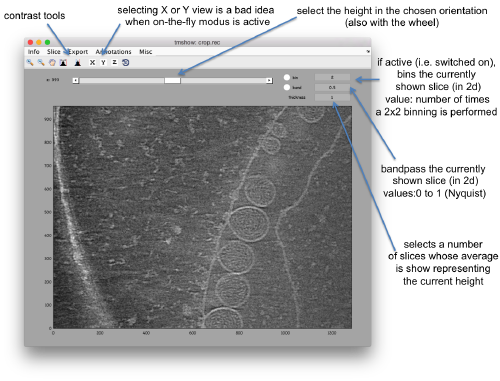
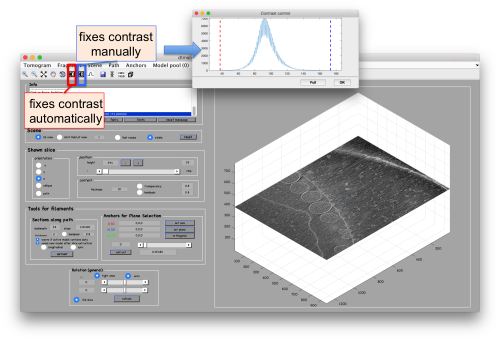
Probably you don't like the initial contrast, change it with the button in the toolbar.
Use the bar to move the slice up and dow, or drag it with the cursor while keeping the main mouse button pressed. Other axiliary tools are the keys x,y,z to change the slice orientation, the number of projected slices (called "thickness" in the GUI controls).
Creation of models to contain annotations
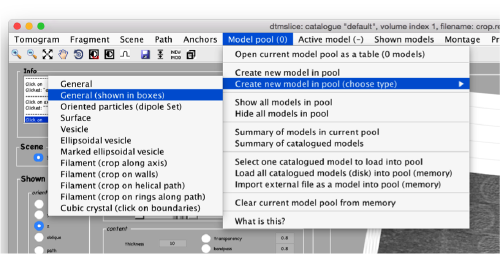
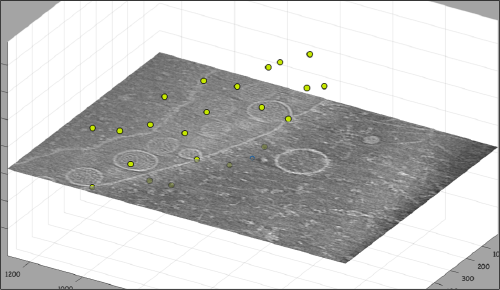
In this example we just want to manually pick some particles. This can be done creating a general or box model, which will reside in memory till we save it into the catalogue.
After creating the model, it will be only model currently active in the dtmslice scene. You can add new points pressing on [c]. The idea is to mark on the positions where you see the "neck" of a vesicle (what we called "crowns") in contact with the outer mithocondrial membrane.
The last marked point can be deleted by pressing [delete]. An arbitrary point can be deleting by clicking on it with the auxiliary mouse button. This will open a menu that includes the option of deleting the point (through Ctrl+X in Linux or Cmmd+X in Mac).
At this stage you probably want to change the transparence of the depicted slice, so that you can control which objects have been already clicked below the depicted slide.
.
When you are done, remember to save the model, using the menu options on active model or simply clicking on the disk icon in tomoslice.
Cropping particles
Now we want to use the positions that we have marked to extract the subtomograms and format them as a data folder. The first thing we nee is an estimation of the sidelength in pixels of each of the subtomograms. In dtmslice We can use the keys [1] and [2] to define two anchor points that appear as rombohedra. Clicking (with the right button) onto the black dashed that links the will show on screen both coordinates and the distance between them. All distances are reported in pixels of the not-binned tomogram: even if you are using any un-binned version, Dynamo keeps track of it.
.
We will thus choose to create a datafolder with a cubic sidelength of 128 pixels (remember that the particles will be cropped in the unbinned tomogram). This will ensure that the crowns fit comfortably inside the physical box, even if our manual picking imposes an error of several pixels. If you were using, say, a thickness parameter of 10 pixles in dtmslice, you have to count with at least this inaccuracy in the location of the particles.
Now, we check that the catalogued tomogram contains the model that we manually picked before:
>> dcmodels fhv Volume 1 contains 1 models in total /Users/casdanie//fhv/tomograms/volume_1/models/mboxes.omd
Creating a table
We could just use the catalogue GUI to extract the particles, be it is also possible top roceed directly with the command line. We will use the dtcrop command, .which requires preparing a table with the information of the model.
m = dread('/Users/casdanie//fhv/tomograms/volume_1/models/mboxes.omd');
t = m.grepTable();
Here, you read the file into a model object (which we arbitrarily choose to call m), and then you use the grepTable method on this object to extract a variable into your workspace. We arbitrarily call it t.
Note that we can extract models directly from the output of dcmodels
dcmodels fhv -i 1 -ws o;
m = dread(o.files{1});
t = m.grepTable();
i.e., we load the answer of dcmodels for volume index -i 1in the output variable o . Inside it, there is a field called 'files' which contains a cell array of files containing models. Then we read the first entry o.files{1}.
Whichever way you create the table variable t, it is just a matrix with a row for each particle, and a summary of the information coded inside can be created through:
</nowiki>>>dtinfo(t);
size : 22 35
NaNs : 0
COLUMN
[ 2 ] marked for alignment: 22 [ 3 ] included in average : 22 [ 4-6 ] shifts : all zero [ 7-9 ] angles : all zero [ 10 ] cross correlation : min: 0.00 max: 0.00 mean: 0.00 std: 0.00 [ 13 ] Fourier sampling : 1 (single tilt around y) [ 13 ] fsampling types : all of the same type [14-15] ytilt range : min:120.00 max:120.00 [16-17] xtilt range : min:120.00 max:120.00 [ 20 ] linked volumes : total 1 (labels: [1]) [ 21 ] regions inside tomograms : total 1 (labels: [0]) [ 22 ] user-defined classes: total 1 (labels: [0]) [ 23 ] annotation types : total 1 (labels: [0]) [24-26] spatial locations : initialized: 22 [ 24 ] * x : min: 645.21 max: 1001.92 mean: 799.05 std: 109.44 [ 25 ] * y : min: 23.78 max: 917.51 mean: 484.07 std: 271.28 [ 26 ] * z : min: 198.00 max: 563.00 mean: 415.55 std: 114.03 [ 31 ] original tags : total 1 (labels: [0]) [ 32 ] compacted particles : total 1 (labels: [1]) [ 34 ] references : total 1 (labels: [0]) [ 35 ] subreferences : total 1 (labels: [0]) [ 36 ] apix : Warning: column not available in this table [ 37 ] defocus : Warning: column not available in this table</nowiki>
Using dtcrop
The simplest syntax of dtcrop<t/t> requires passing the name of the tomogram from which we want to crop (syntax varies for cropping from multiple tomograms). We know that the file is crop.rec, and we could directly insert this name in the command. But a catalogued model already contains information about its source tomogram (inside its property cvolume, so that we can always track it back. We could then define a variable
tomogramFile = m.cvolume.file();
and launch the cropping order
o = dtcrop(tomogramFile,t,'particlesData',128);
where you could add the mw flag to let Dynamo use several cores. In any case, for this number or particles the cropping should take some seconds. The last part of the final output into screen should look like this:
21 [read_subtomogram] Volume has size 1285 956 786
[read_subtomogram] Accessing subvolume x: 713:840; y: 339:466; z: 160:287 totalling ~ 16.0Mb
Elapsed time is 0.191014 seconds.
22
Total time invested in cropping: 7s
[table_crop] Done extracting 20 particles
from tomogram :"/Users/casdanie/dynamo/devmac/workplace/paris/crop.rec"
destination folder :"particlesData"
excluded particles : 2
[ok] table_crop
informing you that some of the particles where excluded, as they were probably too close to the boundary of the tomogram, given the sidelength we asked for. Inside the created data folder,
you will find the table particlesData/crop.tbl, which only indexes the actually cropped particles.
Creating an average
The particles can now be averaged together. They have different orientations, but in this tomogram we only have a fraction of the membrane.
oa = daverage('particlesData','t','particlesData/crop.tbl');
If you want to let Dynamo pass maps into Chimera, you have to inform Dynamo on the location of Chimera.
dchimera -path /Applications/Chimera.app/Contents/MacOS/chimera
Project to find membrane orientations
We first need to create files with the average and the table that we have till now in memory:
dwrite(t,'raw.tbl'); dwrite(oa.average,'rawTemplate.em');
We can create a project directly thorugh the command line:
dcp.new('first','d','particlesData','template.em','rawTemplate.em','masks','defaults','t','particlesData/crop.tbl');
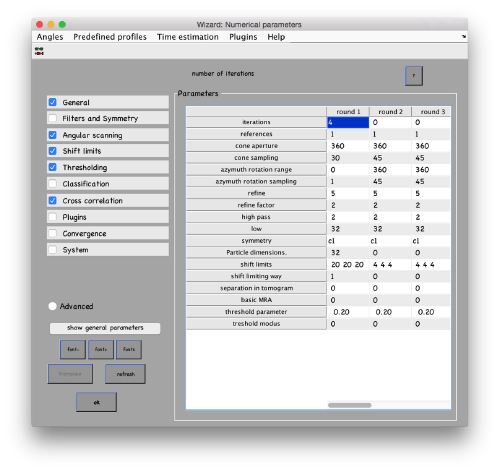
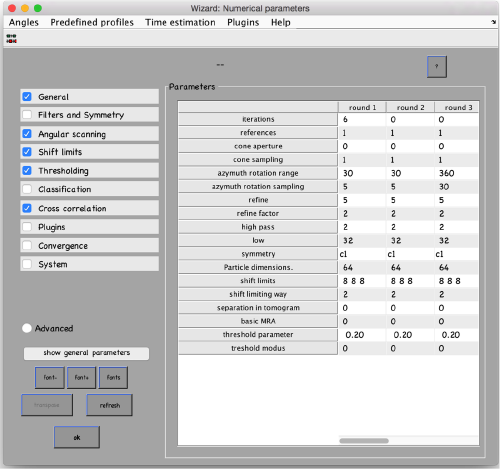
...and go directly to the panel of numerical parameters to create a project adapted for catching the general orientation of the membrane:
mbparse.multicore.checkPhysicalCores
Your project invokes multicore operations (2 cores required). Dynamo will now test your hardware to check that it can run the project. Starting parallel pool (parpool) using the 'local' profile ...
After running the project, we check the created average:
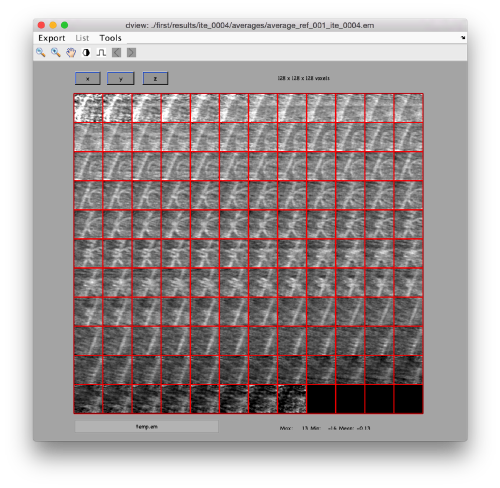
ddb first:a -v
This command asks the database (hence db) of the project first to look for the item of type average, by default accessing the last computed one. The flag -v sends the output of the database query to the depiction GUI called dview.
.
Apparently, the project finds the membranes and centers the particles correctly. If you show the volume in Chimera (by clicking in the Export>Send to Chimera option in the dview window ).
.
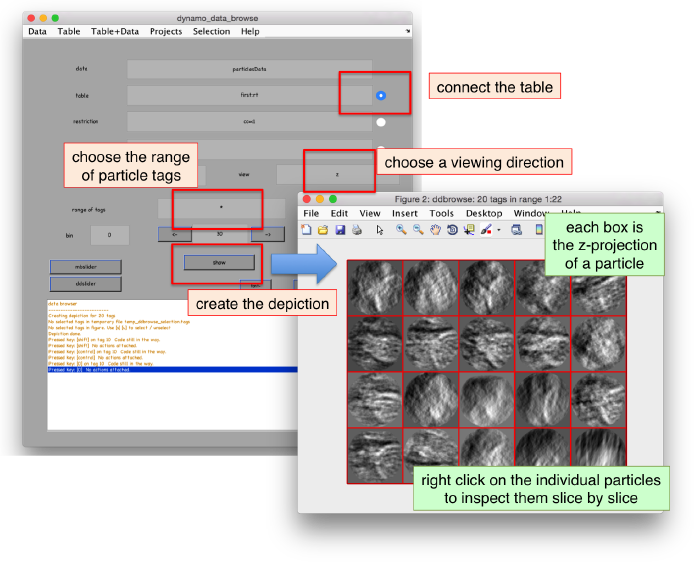
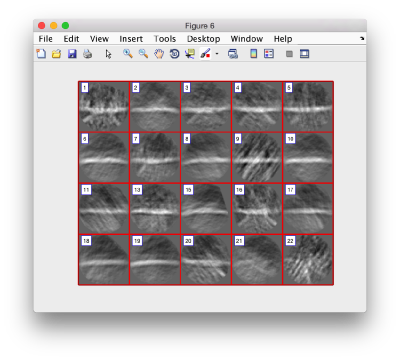
We can check the individual particles:
ddbrowse -d first:data -t first:rt
.
Aligning the axis of symmetry
We would like to bring the axis of symmetry to the zdirection. This will create an intuitive separation between the two first euler angles that represent "change of orientation of the main axis", and the third one that represents "azymutal rotation about the new axis". We want that azymtal rotations occur about an axis of possible symmetry, which by convention is located along z. There are several ways to achieve this. A simple one is to create a model of the membrane/crown geometry, align our average to it (with dalign), and use the alignment parameters to create a new table. With this new table and average we will be able study possible symmetries with a new project.
Creating a template aligned with z
Geometrical shapes of many types can be created with dmask,dsphere,dcylinder,dshell and dtube, and combined with dynamo_mask_combine. However, there are also some available utilities to create templates representing frequently occurring membraneous geometries:
mr = dpktomo.examples.motiveTypes.MembraneWithRod(); mr.sidelength = 128; mr.rodRadius = 20; mr.rodShift = [0,0,10];mr.rodHeight= 10; mr.getMask(); template = mr.mask;
We can check the result with:
mr.viewMask();
Aligning the previous average along z
The mask is white on black by definition. The tomogram data in this case represents bright protein on dark background, so that in this case we want to align the previously comptued average to the mask of the mr object.
The alignment does not need to scan azymutal rotations, so that our 'inplane_range' will be 0. The 'cone_range' will be the full sphere, and we take and spacing of 30 degrees. As we are looking for coarse orientations, we can bin the two volumes twice (yielding volumes with a sidelength of 32 pixels). We also "nail" the new center to the physical center of the box.
Now we read the average computed by the project first into a workspace variable which we arbitrarily call previousAverage
ddb first:a -r myParticle;
previousAverage is treated as a "particle" to be aligned onto a template, which in this case is the volume contained in mr.mask. sal = dalign(previousAverage,mr.mask,'cr',360,'cs',30,'ir',0,'dim',32,'limm',1,'lim',[10,10,10]);
The flags are the same parameters that would be used in an alignment project. You can check the shorthands with dvhelp.
The output result sal contains many fields. We can, for instance directly visualize how the previous average looks like when transformed through the results of this dalign operation.
Applying the z-alignment to the table
We don't want just to get a z-oriented average: we also want to convert the table yield by the first project into a table that, when applied onto the original data, produces a correct, z-aligned average. For this, we use the alignment parameters coded inside the output sal (as field .Tp) and apply them onto the table.
ddb first:rt -r tf
The variable tf contains now the original table, which is now rotated and shifted according with the rigid body transform Tp inside sal
tr = dynamo_table_rigid(tf,sal.Tp);
now the rectifiedtable tfz should contain the metadata that makes the particles "point upward". We use now the typical sanity check to assess that a table behave as expected: we apply it to the particles in its paired data folder and check the average.
oz = daverage('first:data','t',tr,'fc',1);
whose results can be checked by:
dview(oz);
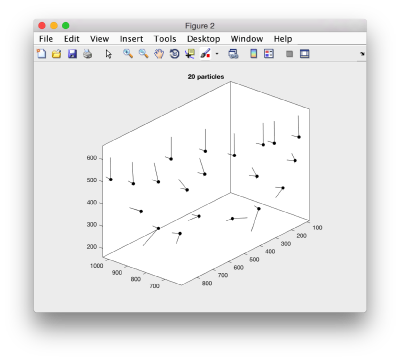
We can visualize this operation by plotting an sketch with the orientation of the particles. We first show the results for the table computed in the project first
figure; dtplot('first:tr','m','sketch','sketch_length',100,'sm',30); view(-230,30);axis equal;
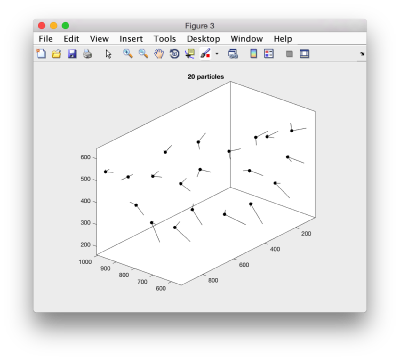
Here, the 'z' orientation computed for each particle is represented by the longest semiaxis. Note that with the original definition of the template, the 'z' points -approximately- along the direction of the 'z' in the tomogram. If we depict the same plot with the table we just computed:
figure; dtplot(tr,'m','sketch','sketch_length',100,'sm',30); view(-230,30);axis equal;
we see that now the 'z' axis in each particle is pointing orthogonally(-ish) to the membrane. A different quick check would be to show the projections of the particles along y. Instead of using the GUI ddbrowse, we can create this depiction with a single command:
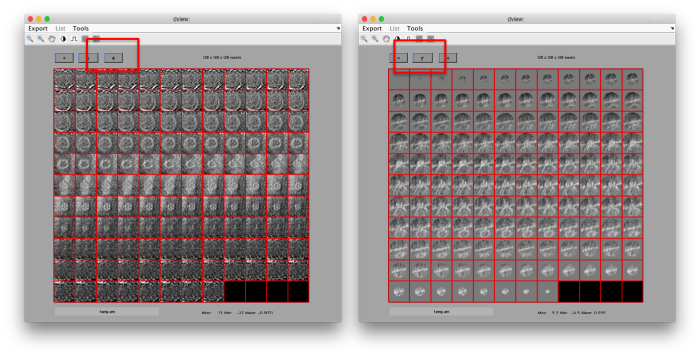
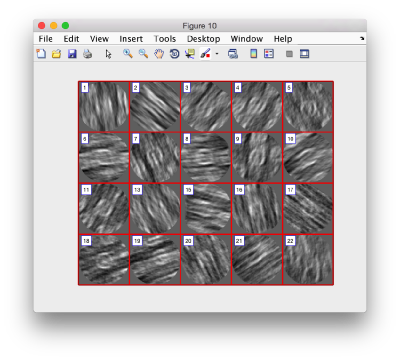
figure;dslices('particlesData','t',tr,'projy','*','align',1,'labels','on');
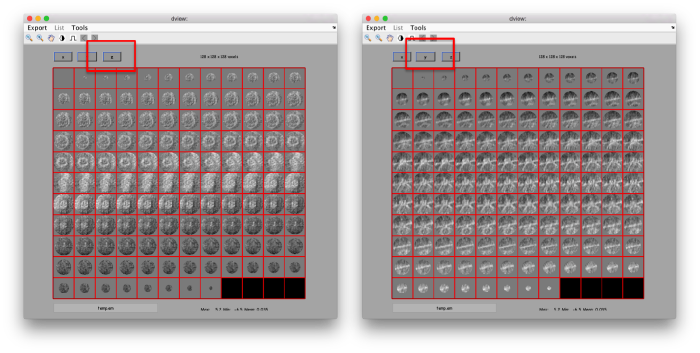
Lets look at the z-projection. In this case we project only the central slices around the crown and the aperture in the viral vesicle, chosing thus slices 60 to 70. if project the full particle, we won't distinguish any features.
figure;dslices('particlesData','t',tr,'projz',60:80,'align',1,'labels','on');
The depiction clearly shows the missing wedge of the particles. Incidentally, it also shows that averaging all the particles should produce an average that covers all the orientaions in the Fourier space.
Project for rotational alignment
We have now a template and a coherently defined metadata (i.e. table) that align the particles coarsely along the right direction. We write them into disk:
dwrite(tr,'Oriented.tbl'); dwrite(oz.average,'zOriented.em');
and create a project with these files. Note that the data folder remains unchanged.
dcp.new('first','d','particlesData','template','zOriented.em','masks','default','t','zOriented.tbl');
In this project, we will ask for a symmetrization 'c57'.. this is just to simulate fully rotational symmetry. We are not assuming that this symmetry is physical: we just want to force any possible symmetry axis in the data along the z axis. We also keep binning twice the particles, in order to get the computation times short.
Project with rotational randomization
We can create a template that does not have a prefererential orintation, by just randomizing the azymutal rotations in our table, We extract the last refined table
ddb zNonSymmetric:rt -tns
and impose a perturbation that keeps all other parameters constant but randomly rotates the particles around their axis
tr = dynamo_table_perturbation(tns,'pshift',0,'paxis',0,'pnarot',360);
We can use this table to average again the particles and check the average.
oar = daverage('particlesData','t',tr,'fc',1);
dview(oar)
Now, we can write these files in disk and create a project: dwrite(oar.average,'randomizedAverage.em'); dwrite(tr,'randomized.tbl'); dcp.new('zRandomized','d','particlesData','template','randomizedAverage.em','masks','default','t','randomized.tbl');
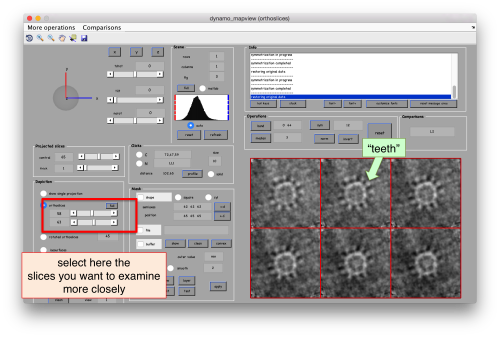
The presence of a crown-like is very, ver faintly hinted in mapview
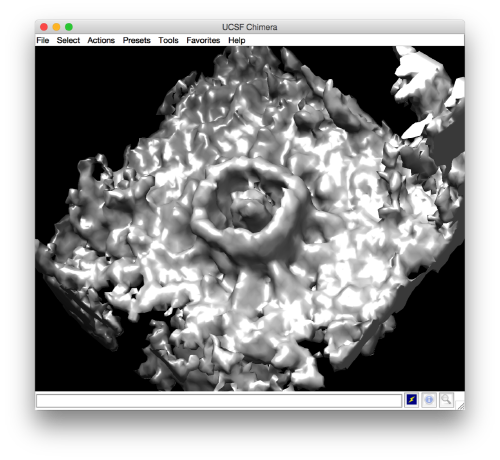
and barely identifialble in Chimera:
Project for localized alignment
We don't see clearly what is happening on the area of interest... On one hand we know that we are using a very reduced number of particles ( which on top of it are too similarly oriented). But there is still some room to improve in the approach: we can focus the refinement in the area of interest.
Creating a tight mask
We want to create a mask that encloses the area of interest. To this end, we open the average in dmapview, by transferring it from dview (Export) or just asking ddb to pass the average directly to mapview
ddb zRandomized:a -m
We tune the browser for viewing along y, and we select one of the central slices. We can use a thickness of several pixels to have a better view.
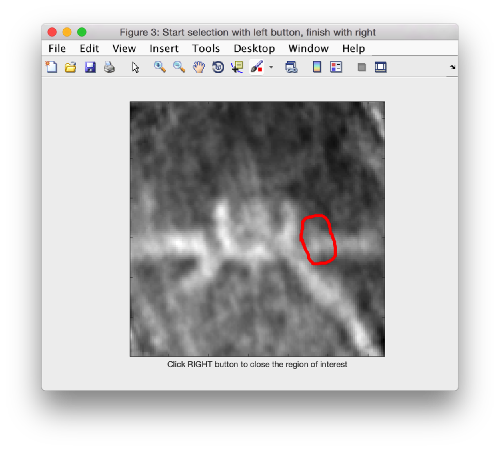
The we select the area that we want to use as seed in this plane to create a revolution solid. We press on [shift] + [s] on the selected slide, letting a new window pop up.
We have to change the default name given by Dynamo to this mask.
!mv temp_drawn_revolution_mask.em teethMask.em
and now continue the previous project by transferring the results of zRandomized to a fresh project (lets call it localized)
dynamo_vpr_branch zRandomized localized -b 1 -noise 0
where we insert the tight mask teethMask.em that we just created as alignment mask of the project. Note that we do not want impose any symmetry in our parameters:
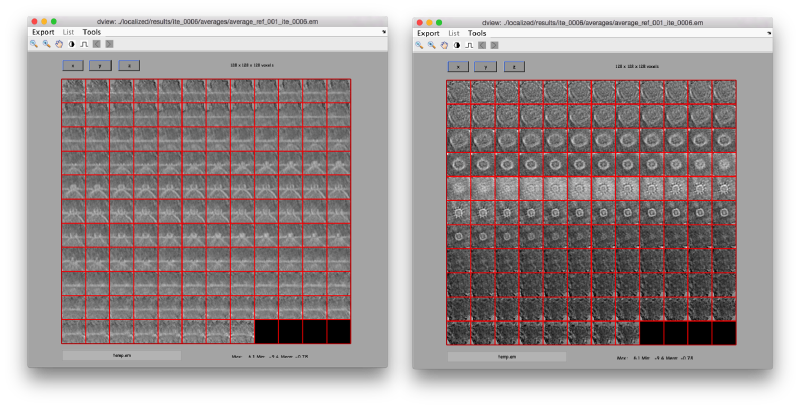
Let's inspect the output in dview
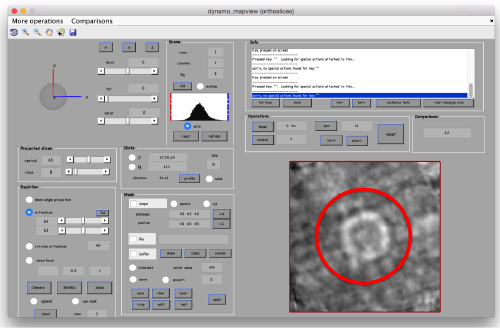
There are different things that we like in this average
- The localized masking worked well, producing a clearer insight into the region of relevance
- Although we are using signal only inside the mask, the material outside of the mask does 'not become smeared. This is clear mark that the alignment is real and non artifactual. That's an important point to check when we use small masks.
- The symmetry in the area becomes apparent on the bare eye. They can be distinguished clearly with mapview and even in Chimera.