Difference between revisions of "Walkthrough on localized reconstruction"
| Line 34: | Line 34: | ||
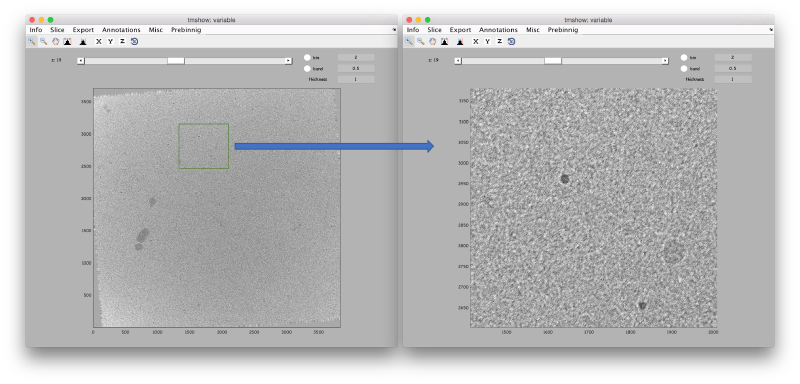
<tt>dtmshow(ts)</tt> | <tt>dtmshow(ts)</tt> | ||
| − | [[ | + | [[ File:LocalizedProjectionDtmshowFullZoomed.png |thumb|center|800px| <tt>tmshow</tt> of raw tilt series ]] |
==== Prebinning during inspection ==== | ==== Prebinning during inspection ==== | ||
| Line 47: | Line 47: | ||
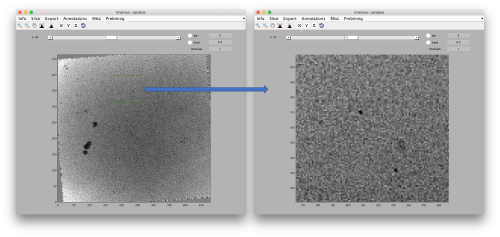
<tt>dtmshow(ts,'bz',3)</tt> | <tt>dtmshow(ts,'bz',3)</tt> | ||
| − | [[ | + | [[ File:LocalizedProjectionDtmshowBinnedZoomed.png |thumb|center|500px| <tt>tmshow</tt> of 3x binned tilt series ]] |
=== Geometric conventions === | === Geometric conventions === | ||
| Line 69: | Line 69: | ||
In this walkthrough, we use Weighted Backprojection as reconstruction algorithm. We apply here the simplest possible filter onto the original projections: a ramp filter. | In this walkthrough, we use Weighted Backprojection as reconstruction algorithm. We apply here the simplest possible filter onto the original projections: a ramp filter. | ||
| − | <tt> | + | <tt>sf = dpktomo.applyRampFilter(sbin)</tt> |
=== Reconstruction === | === Reconstruction === | ||
| Line 76: | Line 76: | ||
By default, the center of the reconstructed volume will be located at the stack 3d center. | By default, the center of the reconstructed volume will be located at the stack 3d center. | ||
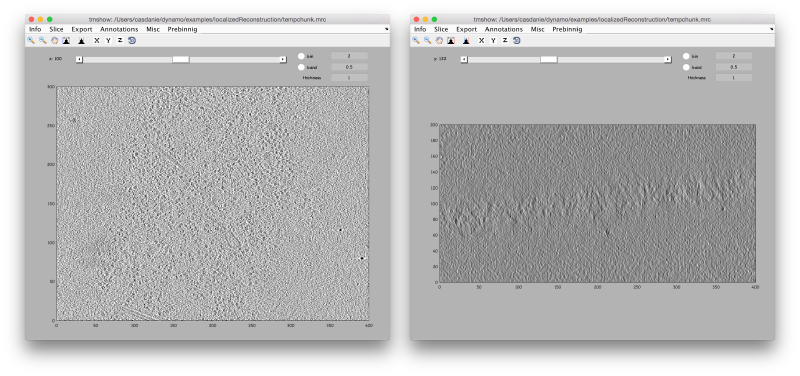
| − | <tt> obp = dpktilt.math.backproject([400,400,300], | + | <tt> obp = dpktilt.math.backproject([400,400,300],sf,tiltAngles);</tt> |
The output <tt>obp</tt> contains the reconstructed volume (as field <tt>v</tt>), and other information, including a description of the geometrical relationship between the reconstucted volume and the tilt series. We will use this information later. | The output <tt>obp</tt> contains the reconstructed volume (as field <tt>v</tt>), and other information, including a description of the geometrical relationship between the reconstucted volume and the tilt series. We will use this information later. | ||
| + | |||
| + | [[ File:LocalizedProjectionDtmshowRec.png |thumb|center|800px| <tt>tmshow</tt> on the reconstruction, ''z'' and ''x' views ]] | ||
==== CTF considerations ==== | ==== CTF considerations ==== | ||
| Line 208: | Line 210: | ||
=== Full resolution reconstruction === | === Full resolution reconstruction === | ||
| + | Now can proceed to transport the locations annotated in the 3x binned geometry into the full size information. | ||
| + | |||
| + | <tt>fgb = fbp.localReconstruction(gb(1,:)*2^3,[60,60,60],sRamp); </tt> | ||
| + | |||
| + | The localized reconstruction can be shown through: | ||
| + | <tt>fgb.view</tt> | ||
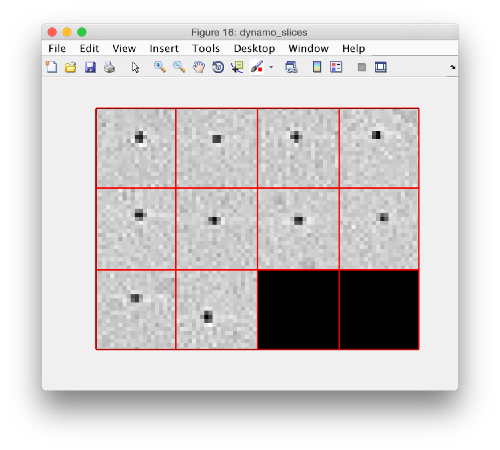
[[ File:LocalizedWBPlocalReconstruction1Full.png |thumb|center|500px| Single gold bead, full resolution ]] | [[ File:LocalizedWBPlocalReconstruction1Full.png |thumb|center|500px| Single gold bead, full resolution ]] | ||
| + | |||
| + | Note that we don't really need to use the object <tt>fgb</tt> as support. Its only role is to work out the geometry, computing the position of the 3d stack center with reference to the subtomogram that we want to reconstruct locally. We can work out the maths and compute the vector: <tt>[1035.431 551.378 318.140] </tt>. We could use this vector directly in <tt>dpktilt.math.backproject</tt> | ||
| + | and get the same result. | ||
| + | |||
| + | <tt>fbpDirect = dpktilt.math.backproject([60,60,60],sRamp,tiltAngles,'sc',[1035.431 551.378 318.140]);</tt> | ||
| + | |||
| + | We can now reconstruct all the gold beads at full resolution. | ||
| + | <tt>fbp.reconstructIntoDataFolder('fullGoldBeads',80,sRamp,'points',gb*8,'fo',1); </tt> | ||
| + | |||
| + | and create a depiction of the data set. | ||
| + | <tt>figure;dslices fullGoldBeads z -j * </tt> | ||
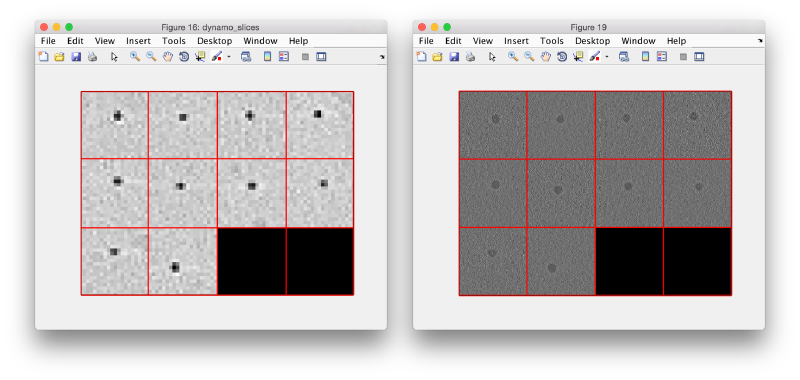
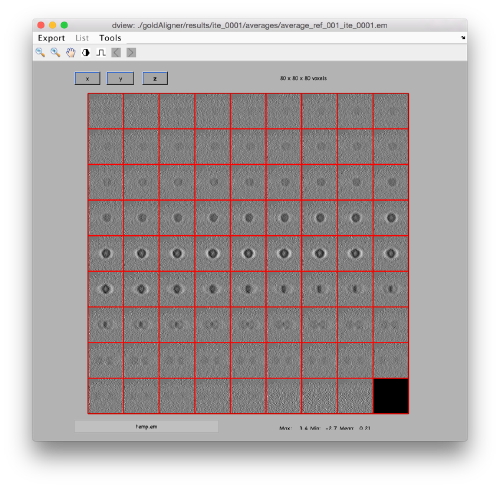
[[ File:LocalizedWBPlocalReconstructionAllFullCompare.png |thumb|center|800px| All gold beads, full resolution ]] | [[ File:LocalizedWBPlocalReconstructionAllFullCompare.png |thumb|center|800px| All gold beads, full resolution ]] | ||
| Line 215: | Line 234: | ||
=== Refining the full resolution reconstruction === | === Refining the full resolution reconstruction === | ||
| − | [[ File:LocalizedWBPlocalReconstruction1FullRecentered.png |thumb|center|500px| | + | Now, we could find the actual positions of the gold beads with an alignment project. We create a spherical template and mask: |
| + | |||
| + | <nowiki> | ||
| + | dwrite(-dsphere(10,80),'template.mrc'); | ||
| + | dwrite(dsphere(16,80),'mask.mrc'); | ||
| + | dwrite(dynamo_table_blank('fullGoldBeads'),'blankFull.tbl'); </nowiki> | ||
| + | ddelete goldAligner | ||
| + | dcp.new('goldAligner','d','fullGoldBeads','t','blankFull.tbl','template','template.mrc','mask','mask.mrc','show',0); | ||
| + | dvput goldAligner -cr 0; | ||
| + | dvput goldAligner -ir 0; | ||
| + | dvput goldAligner -rf 0; | ||
| + | dvput goldAligner -lims 40; | ||
| + | dvput goldAligner -ite 1; | ||
| + | dvput goldAligner -dim 80; | ||
| + | check = dvcheck('goldAligner'); | ||
| + | |||
| + | If the check doesn't report any problem, we can then just unfold the project: | ||
| + | |||
| + | <nowiki> dvunfold goldAligner | ||
| + | goldAligner</nowiki> | ||
| + | |||
| + | Then we can check the result. | ||
| + | |||
| + | <nowiki>ddb goldAligner:a -v </nowiki> | ||
| + | |||
| + | The resulting gold bead is now centered | ||
| + | |||
| + | [[ File:LocalizedWBPlocalReconstruction1FullRecentered.png |thumb|center|500px| Averaged gold bead (centered)]] | ||
| + | More importantly, the ''individual'' gold beads are now centered: | ||
| + | [[ File:LocalizedWBPlocalReconstruction1FullRecentered.png |thumb|center|500px| Averaged gold bead (centered)]] | ||
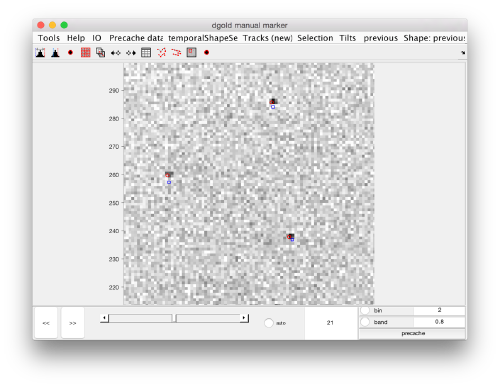
[[ File:LocalizedWBPMarkersAligned.png |thumb|center|500px| New set of markers in 2d (red)]] | [[ File:LocalizedWBPMarkersAligned.png |thumb|center|500px| New set of markers in 2d (red)]] | ||
[[ File:LocalizedWBPMarkersAlignedZoom.png |thumb|center|500px| Raw set of markers (blue) ]] | [[ File:LocalizedWBPMarkersAlignedZoom.png |thumb|center|500px| Raw set of markers (blue) ]] | ||
Revision as of 12:15, 6 November 2017
ARTICLE IN CONSTRUCTION, SORRY
In this walkthrough, we use localized reconstruction to reconstruct a set of subtomograms at full pixel resolution without the requirement of creating a full reconstruction first. In this approach, we:
- create a reconstruction at low resolution
- mark the coordinates of interest in the low resolution reconstruction
- reconstruct separately the different coordinates at full resolution
For the sake of simplicity, in this walkthrough, the landmarks of interest will be simply the gold beads, which are trivially recognizable both in tomograms and in projections in the tilt series.
Contents
Example data set
The data set is an aligned tilt series. No filtering has been performed on it.
Source
The tilt series was used in the publication Cryo-EM structure of the extended type VI secretion system sheath-tube complex (J Wang et. al - Nature microbiology, 2017).
Download tilt series file
The aligned tilt series can be download from:
wget <not yet available>
This will create a file called vc17_align.ali in your current working directory. The tilt angles go from -60 to 60 in intervals of 3 degrees.
The file can be brought into memory through the command
ts = dread('vc17_align.ali');
creating the variable ts (name has been chosen arbitrarily) which contains the tilt series as a numerical matrix.
Inspecting the tilt series
The tilt series at full pixel resolution can be inspected by:
dtmshow(ts)
Prebinning during inspection
You will notice that inspecting the full series in dtmshow is bound to rather slow transitions. It is more convenient to bin the images to a smaller bin level. This can be done by switching on the binning radiobutton. Thus, the accessed slices will be binned on the fl when required.
Note that the coordinates of the axis are kept to the dimension of the unbinned tilt series.
Also, it is possible to create a prebinned version of the stack for different binning levels, so that the slice is accessed already in its prebinned dimension. This can be done after dtmshow has been initialized
or already when starting it (at the cost of an slower initialization)
dtmshow(ts,'bz',3)
Geometric conventions
In Dynamo, we call stack 3d center to a point (xsc, ysc,zsc) univocally defined by a stack of micrographs:
- xsc and zsc and determined by the rotation axis implicitly defined by the alignment.
- ysc is the center of the stack along direction y, defined as floor(Ny/2)+0.5; for a tilt series with Ny pixels along y.
Creation of a binned reconstruction
Binned tilt series
We bin the original tilt series:
ts2 = dpktilt.bin(ts,2)
This command applies a binning of level two to the micorgraphs in the matrix ts separately. Note that the dimensions of the new matrix are floor( [sx,sy]/22<2>).
Filtered tilt series
In this walkthrough, we use Weighted Backprojection as reconstruction algorithm. We apply here the simplest possible filter onto the original projections: a ramp filter.
sf = dpktomo.applyRampFilter(sbin)
Reconstruction
As we have binned the tiltseries, a reconstruction at the full extent of the tomogram will fit easily in memory. We need to chose a size of the output tomogram, expressed in pixels of the stack By default, the center of the reconstructed volume will be located at the stack 3d center.
obp = dpktilt.math.backproject([400,400,300],sf,tiltAngles);
The output obp contains the reconstructed volume (as field v), and other information, including a description of the geometrical relationship between the reconstucted volume and the tilt series. We will use this information later.
CTF considerations
For simplicity, we are skipping the CTF correction step in this walkthrough, where we are only interested in the geometrical manipulations. In a real case, you would just use a version of the tilt series where each micrograph has been phase-flipped according to a defocus estimation computed on the full micrograph.
Annotation on binned reconstruction
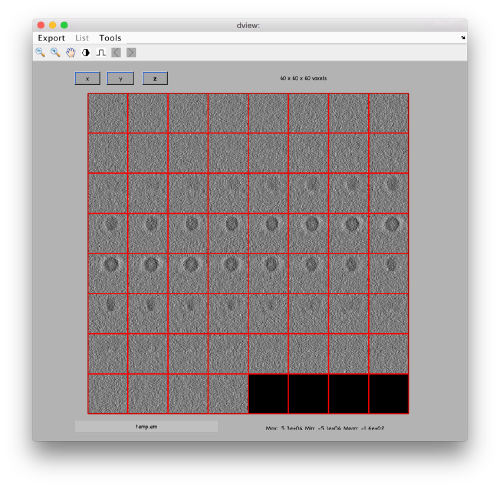
The reconstruction in bin level 2 fits in memory and can be explored easily with dtmslice
We open it creating a catalogue on the fly to contain our annotations:
dtmslice(obp.rec,'in','pr');
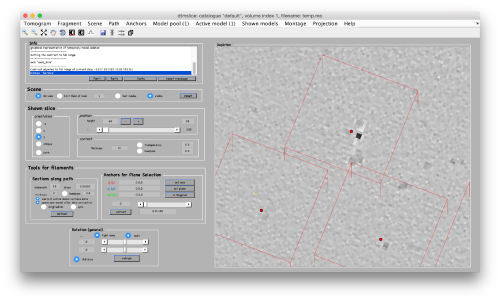
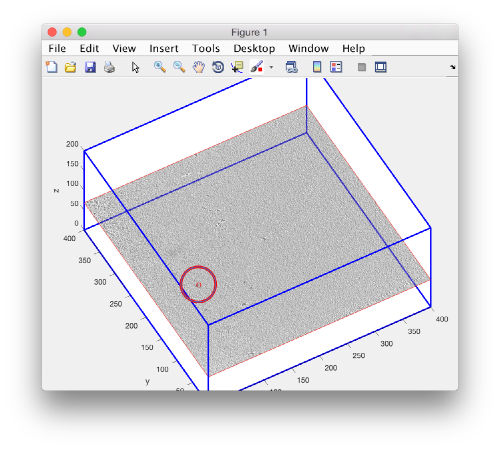
Annotation on 3D
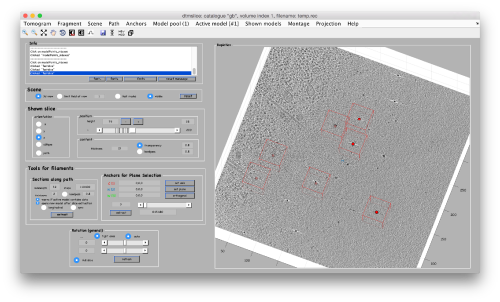
The most trivial strategy for picking particles is to use the 3D viewer. Use C to input a 3d coordinate into the model. Further controls are explained here
Note that you don't need to be very precise to catch the center of the gold bead.
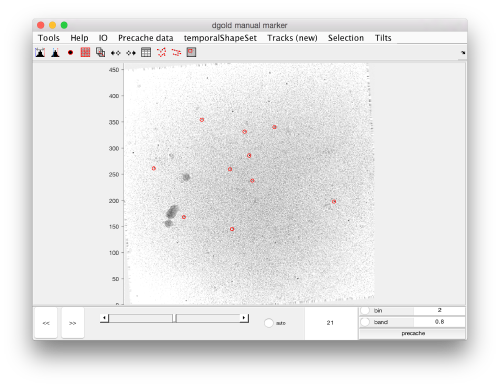
Annotation on projections
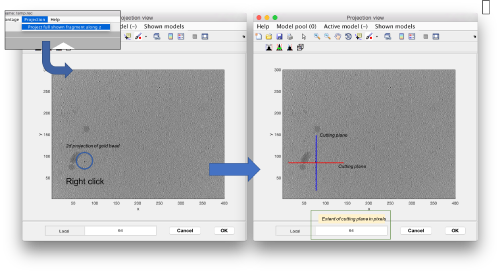
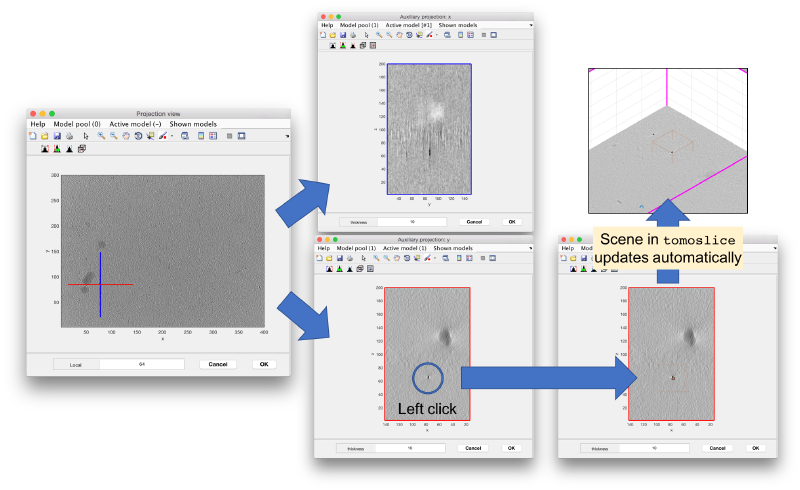
An alternative way to quickly annotate the gold beads is by concurrent projection. In this approach we launch a projection view of the full tomogram [Project > project full shown fragment alongz z].
Two concurrent viewers will pop up showing cuts along x and y, i.e, YZ and XZ planes where the z coordinate can be clicked (in either of them).
The (x,y,z) point will update in the tomoslice window. Also, the windows that show the cuts long x and y will update upon new right-clicks on the z projection.
Saving annotation as model
On either way you chose to perform your annotations (by 3d or by concurrent 2d projections and cut), you can save your model in the catalogue with the disk icon or under the active model menu.
Location of 3d annotations on 2d tilt series
Now we want to localize the 3d coordinates of the gold beads in the binned tilt serie. We first bring the coordinates to a memory variable that we can manipulate. 'If your dtmslice is still open, you can put the points into the workspace memory by Active Model > Export to workspace > Points, which will create in the memory a variable called temp_points with Nx3 entries. Each row are the xyz coordinates of a gold bead.
If you already closed the dtmslice session, you need to read the model that you saved into catalogue:
The points are stored as Nx3 matrix in the points property of the model.
You can check the geometry with low level depicting commands as dslice3d
dslice3d('temp.rec','r',gb(1,:));
hold on;h=dpkgeom.plotCloud(gb(1,:),'or');
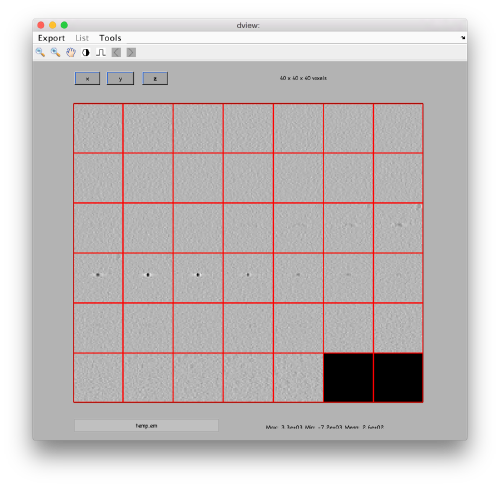
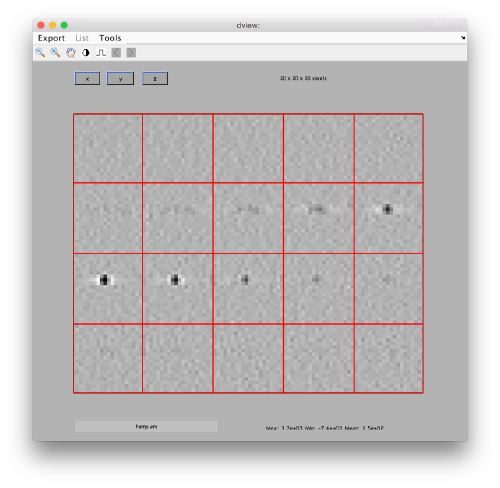
You can also crop a subtomogram around the 3d coordinates and show it as montage of slices with dview
Computation
To find the 2d coordinates of all the goldbeads at once in the micrograph corresponding to a tilt angle of -60, we would write
r2d = dpktilt.point3dInMicrograph(r3d,-60,'sc',[200.5,200.5,100.5],'ss',[sx,sy]);
Note that you need to express the geometric context of r3d.
- 'sc' stands for 'stack3dcenter'
- 'ss' stands for 'stackSize'
In other words, r3d are the coordinates of the point of interest in the reconstructed volume. You need to express how the reconstructed volume related to the original stack dpktilt.point3dInMicrograph needs this information explicitly. Alternatively, you can just use the method 'point3dInAlignedMicrograph' in the obp object, assuming it is still in memory. As this object carries the geometric information, the syntax is simpler.
r2d = obp. point3dInAlignedMicrograph(r3d,-60);
or with the notation {} to pass position in the tilt series.
r2d = obp. point3dInAlignedMicrograph(r3d,{1});
Visualization
Basic Matlab commands
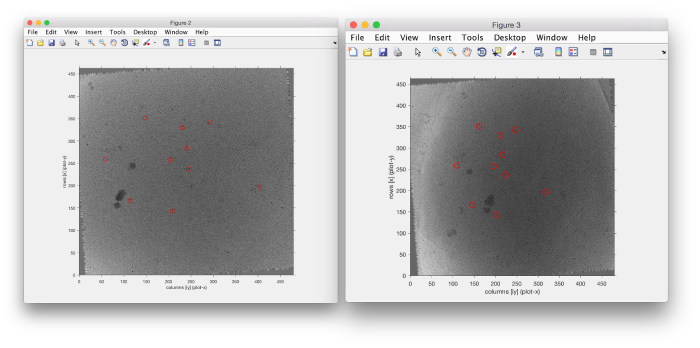
So, did it work? You can check it by just plotting the image of the micrograph
figure(); hi = dshow(sbin(:,:,tilt));
and then plotting on it the positions of the markers.
hold on; h = plot(r2d(:,1),r2d(:,2),'o'); h.LineWidth=1; h.MarkerSize=10; h.Color='r';
Note that the default convention in dshow is to plot the rows of the matrix along the 'x' axis of the plot, with the origin of coordinates in the left bottom corner of the plot. The intensity of matrix entry [i,j] is represented in the pixel centered at (i-0.5,j-0.5).
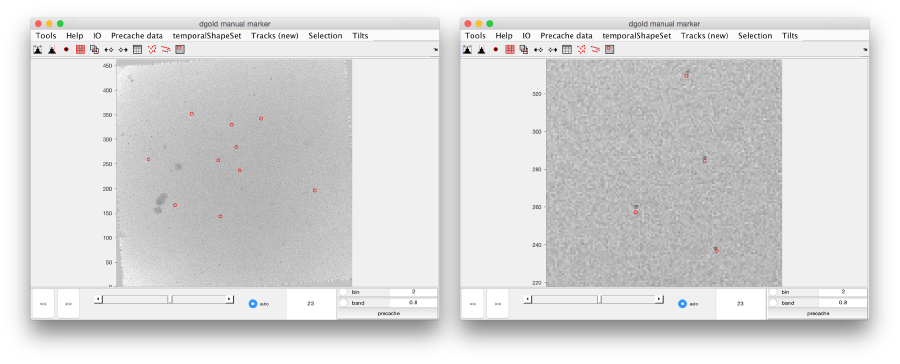
Interactive GUI
The basic tool for visualizing sets of 2d markers defined on a tilt series is dmarkers. This allows to navigate at once through all the annotations on all the images. We first create a shape set for the gold beads:
ss = not yet ready
and open the dmarkers GUI on the tilt series ts3 for this shape set:
gui = dmarkers(ts3,'ss',ss);
Remember that the gold beads had been picked loosely. If you zoom in, you'll see that the red spots are close to but not on the gold bead projections.
Localized reconstruction
Now we want to reconstruct locally each of the gold beads, i.e.
Reconstruct a single area
Reconstruction into a data folder
The command dtrec is the counterpart of dtcrop for tilt series. It loops on the positions inside a table
Full resolution reconstruction
Now can proceed to transport the locations annotated in the 3x binned geometry into the full size information.
fgb = fbp.localReconstruction(gb(1,:)*2^3,[60,60,60],sRamp);
The localized reconstruction can be shown through: fgb.view
Note that we don't really need to use the object fgb as support. Its only role is to work out the geometry, computing the position of the 3d stack center with reference to the subtomogram that we want to reconstruct locally. We can work out the maths and compute the vector: [1035.431 551.378 318.140] . We could use this vector directly in dpktilt.math.backproject and get the same result.
fbpDirect = dpktilt.math.backproject([60,60,60],sRamp,tiltAngles,'sc',[1035.431 551.378 318.140]);
We can now reconstruct all the gold beads at full resolution. fbp.reconstructIntoDataFolder('fullGoldBeads',80,sRamp,'points',gb*8,'fo',1);
and create a depiction of the data set. figure;dslices fullGoldBeads z -j *
Refining the full resolution reconstruction
Now, we could find the actual positions of the gold beads with an alignment project. We create a spherical template and mask:
dwrite(-dsphere(10,80),'template.mrc'); dwrite(dsphere(16,80),'mask.mrc'); dwrite(dynamo_table_blank('fullGoldBeads'),'blankFull.tbl'); ddelete goldAligner dcp.new('goldAligner','d','fullGoldBeads','t','blankFull.tbl','template','template.mrc','mask','mask.mrc','show',0); dvput goldAligner -cr 0; dvput goldAligner -ir 0; dvput goldAligner -rf 0; dvput goldAligner -lims 40; dvput goldAligner -ite 1; dvput goldAligner -dim 80; check = dvcheck('goldAligner');
If the check doesn't report any problem, we can then just unfold the project:
dvunfold goldAligner goldAligner
Then we can check the result.
ddb goldAligner:a -v
The resulting gold bead is now centered
More importantly, the individual gold beads are now centered: