Difference between revisions of "Walkthrough on creation of 3d scenes"
| (20 intermediate revisions by the same user not shown) | |||
| Line 43: | Line 43: | ||
and write it to a file | and write it to a file | ||
| − | <tt>dwrite(t,'alignmentLocalRefinement.tbl')</tt> | + | <tt>dwrite(t,'alignmentLocalRefinement.tbl');</tt> |
==== Template ==== | ==== Template ==== | ||
| Line 49: | Line 49: | ||
Fetch the last computed average | Fetch the last computed average | ||
| − | <tt>ddb localizedFullAngle: | + | <tt>ddb localizedFullAngle:a -r a</tt> |
| + | |||
| + | assuming <tt> localizedFullAngle:a</tt> is the name of your last project. | ||
and write it into disk | and write it into disk | ||
| − | <tt> dwrite( | + | <tt> dwrite(a,'averagedLocalRefinement.em'); </tt> |
==== Membrane model ==== | ==== Membrane model ==== | ||
| Line 67: | Line 69: | ||
So you can read the model into a new variable (arbitrarily called <tt>m</tt>) | So you can read the model into a new variable (arbitrarily called <tt>m</tt>) | ||
| − | <tt>m = | + | <tt>m = dread('Users/casdanie/dynamo/examples/fhvParis/fhv/tomograms/volume_1/models/mySurface.omd');</tt> |
| − | and write it to disk | + | and write it to disk: |
<tt>dwrite(m,'membraneModel.omd');</tt> | <tt>dwrite(m,'membraneModel.omd');</tt> | ||
== Depicting a slice of a tomogram == | == Depicting a slice of a tomogram == | ||
| + | |||
| + | The easiest way is to just use the <tt>dynamo_slice3d</tt> command, which has a simple syntax. For instance, | ||
| + | |||
| + | <tt>o = dslice3d(volume,'r',[40,50,67],'normal','y');</tt> | ||
| + | |||
| + | will create a slice orthogonal to the 'y' direction that cuts the point [40,50,67], and that by definition will have the full extent of the tomogram. This command is a wrapper around the class <tt>dpktomo.volume.slices.Slice</tt>. The rest of this section explains how to use objects of this class to get a detailed level of control of the depictede slice. | ||
=== The slice object === | === The slice object === | ||
| Line 93: | Line 101: | ||
<tt>s.eulers = 'z';</tt> | <tt>s.eulers = 'z';</tt> | ||
| + | |||
| + | You can also input euler triplets as value for property <tt>eulers</tt>. Other properties you can fix are <tt>bandpass</tt> or <tt>thickness</tt>. | ||
Now, we actually compute the slice; | Now, we actually compute the slice; | ||
| Line 98: | Line 108: | ||
<tt>s.fetchData();</tt> | <tt>s.fetchData();</tt> | ||
| − | This will '''not''' create any output in the screen. <tt>fetchData</tt> will just operate the action of visiting the file <tt>crop.rec</tt> and extracting a numeric matrix that represents the gray intensities of the slice with the indicated parameters. The matrix will be stored inside the <tt>s</tt> object (as the <tt>'data'</tt> property) and will be accessed by the depicting operations to be executed later. | + | This will '''not''' create any output in the screen. <tt>fetchData</tt> will just operate the action of visiting the file <tt>crop.rec</tt> and extracting a numeric matrix that represents the gray intensities of the slice with the indicated parameters. The matrix will be stored inside the <tt>s</tt> object (as the <tt>'data'</tt> property) and will be accessed by the depicting operations to be executed later. General help on this class can be found in |
| + | <tt>help dpktomo.volume.slices.Slice </tt> | ||
=== The slice depictor object === | === The slice depictor object === | ||
| − | We first create a figure with and empty axis | + | We first create a figure with and empty axis: |
| − | |||
| − | + | <tt>f = figure; haxis = gca();hold on;</tt> | |
| − | Here, <tt>f</tt> are ''handles'' that will be used later to direct the graphical output to our figure. | + | Here, <tt>f</tt> and <tt>haxis</tt> are ''handles'' that will be used later to direct the graphical output to our figure. |
| + | |||
| + | [[ File:Fhv3dEmptyAxis.png |thumb|center| 400px| Empty matlab figure with an empty axis.]] | ||
Now, we initialize a depiction object associated with the slice <tt>s</tt> | Now, we initialize a depiction object associated with the slice <tt>s</tt> | ||
| − | <tt>sz = dpktomo.volume.slices.SliceGraphic(s);</tt> | + | |
| + | <tt>sz = dpktomo.volume.slices.SliceGraphic(s);</tt> | ||
| + | |||
Note that no graphical output has been created yet. We first inform the object <tt>sz</tt> in which axis it is to be created. | Note that no graphical output has been created yet. We first inform the object <tt>sz</tt> in which axis it is to be created. | ||
| − | <tt>sz.axis.h = haxis;</tt> | + | <tt>sz.axis.h = haxis;</tt> |
and then create the slice in the available axis. | and then create the slice in the available axis. | ||
| Line 125: | Line 139: | ||
or | or | ||
| − | <tt>figure(f);</tt> | + | <tt>figure(f);</tt> |
We can change the angle of view with the rotation icon or programmatically: | We can change the angle of view with the rotation icon or programmatically: | ||
| Line 140: | Line 154: | ||
We first want to crop the available average inside a mask, to get rid of the membrane surrounding the crown. For this we first show the template inside <tt>mapview</tt> | We first want to crop the available average inside a mask, to get rid of the membrane surrounding the crown. For this we first show the template inside <tt>mapview</tt> | ||
| − | <tt>dmapview averagedLocalRefinement.em</tt> | + | <tt>dmapview averagedLocalRefinement.em</tt> |
[[ File:Fhv3dMapviewTemplate.png |thumb|center| 400px| <tt>mapview</tt> on template.]] | [[ File:Fhv3dMapviewTemplate.png |thumb|center| 400px| <tt>mapview</tt> on template.]] | ||
| Line 161: | Line 175: | ||
and apply it onto our template. We apply the 12-fold symmetrization on the same operation. | and apply it onto our template. We apply the 12-fold symmetrization on the same operation. | ||
| − | <tt> | + | <tt> template = dread('averagedLocalRefinement.em');</tt> |
| − | + | <tt> final = dsym(template,'c12').*maskRevolution;</tt> | |
| − | <tt> | + | Here the <tt> A .* B </tt> notation indicates the pixelwise multiplication of two volumes. We can now write the result into a file |
| − | + | <tt>dwrite(final,'placedTemplate.em');</tt> | |
| + | |||
| + | and visualize the result: | ||
<tt>dview placedTemplate.em </tt> | <tt>dview placedTemplate.em </tt> | ||
| Line 183: | Line 199: | ||
Ideally, we would like to export the triangulation created in Chimera into ''Dynamo'' directly (using the ''Export as STL file'' in the ''Export scene'' menu of Chimera). However, you have probably moved and rotated the object in Chimera in order to visualize it more clearly. Thus, we will just use the isolevel computed by Chimera and recreate the isosurface inside ''Dynamo'': | Ideally, we would like to export the triangulation created in Chimera into ''Dynamo'' directly (using the ''Export as STL file'' in the ''Export scene'' menu of Chimera). However, you have probably moved and rotated the object in Chimera in order to visualize it more clearly. Thus, we will just use the isolevel computed by Chimera and recreate the isosurface inside ''Dynamo'': | ||
| − | <tt>dt = dynamo_isosurface( | + | <tt>dt = dynamo_isosurface(final,'isolevel',0.79,'real_isolevel',true,'-show',false);</tt> |
Here, the output <tt>dt</tt> is a ''Dynamo'' object that manages isosurfaces. In order to see the isosurface that we just created, we open a new figure: | Here, the output <tt>dt</tt> is a ''Dynamo'' object that manages isosurfaces. In order to see the isosurface that we just created, we open a new figure: | ||
| Line 191: | Line 207: | ||
and use the <tt>trisurf</tt> command of matlab to open the matlab triangulation contained in the property <tt>tr</tt>. | and use the <tt>trisurf</tt> command of matlab to open the matlab triangulation contained in the property <tt>tr</tt>. | ||
| − | <tt>trisurf(dt.tr);axis equal ; | + | <tt>trisurf(dt.tr);axis equal ; |
[[ File:Fhv3dDynamoTriangulation.png |thumb|center| 400px| Command <tt>trisurf</tt>.]] | [[ File:Fhv3dDynamoTriangulation.png |thumb|center| 400px| Command <tt>trisurf</tt>.]] | ||
| Line 199: | Line 215: | ||
we recover our table with locations '''and'' alignment parameters | we recover our table with locations '''and'' alignment parameters | ||
| − | <tt> t = dread(' | + | <tt> t = dread('alignmentLocalRefinement.tbl'); </tt> |
and create a triangulation object that merges the result of copying, relocating and rotating the isosurface of one template on all positions of the table: | and create a triangulation object that merges the result of copying, relocating and rotating the isosurface of one template on all positions of the table: | ||
| Line 217: | Line 233: | ||
<nowiki>hTriangulation.FaceColor= 'c'; | <nowiki>hTriangulation.FaceColor= 'c'; | ||
hTriangulation.LineStyle = 'none'; | hTriangulation.LineStyle = 'none'; | ||
| − | shg; | + | shg;</nowiki> |
| − | </nowiki> | ||
[[ File:Fhv3dTrisurfNoEdges.png |thumb|center| 400px| <tt>hTriangulation</tt> object after eliminating the depiction of the edges]] | [[ File:Fhv3dTrisurfNoEdges.png |thumb|center| 400px| <tt>hTriangulation</tt> object after eliminating the depiction of the edges]] | ||
| Line 224: | Line 239: | ||
The object is indeed cyan, but we don't see any details, as we haven't defined any shading: | The object is indeed cyan, but we don't see any details, as we haven't defined any shading: | ||
| − | <nowiki>axis equal; | + | <nowiki>axis equal; |
f.Name = 'Simple trisurf scene'; | f.Name = 'Simple trisurf scene'; | ||
% just m the exploration | % just m the exploration | ||
| Line 231: | Line 246: | ||
shading(haxis,'faceted'); | shading(haxis,'faceted'); | ||
l = lightangle(-45,30); | l = lightangle(-45,30); | ||
| − | shg<nowiki> | + | shg</nowiki> |
[[ File:Fhv3dTrisurfLighting.png|thumb|center| 400px| addition of a light source]] | [[ File:Fhv3dTrisurfLighting.png|thumb|center| 400px| addition of a light source]] | ||
| Line 244: | Line 259: | ||
Now we repaint the triangulation to cyan. | Now we repaint the triangulation to cyan. | ||
| − | <tt>hTriangulation.FaceColor= 'c'; </tt> | + | <tt>hTriangulation.FaceColor= 'c'; </tt> |
[[ File:Fhv3dTrisurfColormapCyan.png |thumb|center| 400px| Using a single color for the whole triangulation]] | [[ File:Fhv3dTrisurfColormapCyan.png |thumb|center| 400px| Using a single color for the whole triangulation]] | ||
| Line 252: | Line 267: | ||
If you want to change an existing slice on an already created scene, you need to change some settings. | If you want to change an existing slice on an already created scene, you need to change some settings. | ||
| − | < | + | <nowiki>s.refresher.dataUpdatesAfterGeometryChanges(); |
| − | sz.surface.autoUpdate();</ | + | sz.surface.autoUpdate();</nowiki> |
After them, any change in <tt>thickness</tt>, <tt>band</tt>,<tt>center</tt>,<tt>l</tt>,<tt>eulers</tt> will automatically refresh the appearance of the slice, For instance you can shift it upwards through: | After them, any change in <tt>thickness</tt>, <tt>band</tt>,<tt>center</tt>,<tt>l</tt>,<tt>eulers</tt> will automatically refresh the appearance of the slice, For instance you can shift it upwards through: | ||
| Line 277: | Line 292: | ||
and extract the triangulation hidden inside it (<tt>mesh.tr</tt> property) | and extract the triangulation hidden inside it (<tt>mesh.tr</tt> property) | ||
| − | < | + | <tt>hMem =trisurf(m.mesh.tr);</tt> |
We may want to adjust the appearance a little, for instance the transparence: | We may want to adjust the appearance a little, for instance the transparence: | ||
Latest revision as of 11:46, 29 November 2017
This walkthrough shows how to create graphic depictions of tomogram contents. Those include:
- Slices of tomograms.
- Proteins located in the tomogram, with the orientations provided during the alignment.
- Geometrical objects (as membranes represented by triangulations).
Contents
The data set
This walkthrough works with the data set from the advanced starters guide. The goal is to depict:
- One slice of the tomogram in 3D.
This requires a tomogram file. - The viruses placed an oriented along the directions found during a previous computed average.
This requires a template represe. - A sketch of the membrane
This requires a model object.
From the Dynamo web
The tomogram can get fetched through:
wget https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/fhv/crop.rec
in a linux shell, or through:
curl -O https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/fhv/crop.rec
under MacOS.
The table, template and membrane model can be fetched similarly with names
https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/fhv/alignmentLocalRefinement.tbl https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/fhv/averagedLocalRefinement.em https://wiki.dynamo.biozentrum.unibas.ch/w/doc/data/fhv/membraneModel.omd
From your previous work
Assuming you have done the tutorial on the FHV data set, you can use the elements that you have already computed. Just extract them from the best project that you completed. Do not use a subboxing project: we want to get a template for the full crown. Examples below are given assuming that your best project was named localized, substitute if not.
Table
Recover the last computed refined table in the data base of your project
ddb localized:rt -r t
and write it to a file
dwrite(t,'alignmentLocalRefinement.tbl');
Template
Fetch the last computed average
ddb localizedFullAngle:a -r a
assuming localizedFullAngle:a is the name of your last project.
and write it into disk
dwrite(a,'averagedLocalRefinement.em');
Membrane model
If you created manually a membrane model, it should be inside your catalogue with the name mySurface (or any other you put). You can check inside the catalogue fhv:
dcmodels fhv -nc mySurf
Here -nc mySurf will look for models with the string "mySurf" in the name. You should get a reply as:
Volume 1. Matching models: 1 (total: 1) /Users/casdanie/dynamo/examples/fhvParis/fhv/tomograms/volume_1/models/mySurface.omd
So you can read the model into a new variable (arbitrarily called m)
m = dread('Users/casdanie/dynamo/examples/fhvParis/fhv/tomograms/volume_1/models/mySurface.omd');
and write it to disk:
dwrite(m,'membraneModel.omd');
Depicting a slice of a tomogram
The easiest way is to just use the dynamo_slice3d command, which has a simple syntax. For instance,
o = dslice3d(volume,'r',[40,50,67],'normal','y');
will create a slice orthogonal to the 'y' direction that cuts the point [40,50,67], and that by definition will have the full extent of the tomogram. This command is a wrapper around the class dpktomo.volume.slices.Slice. The rest of this section explains how to use objects of this class to get a detailed level of control of the depictede slice.
The slice object
s = dpktomo.volume.slices.Slice();
Here s is just an object that will read data from a tomogram file to be defined, along with geometrical parameters as center, eulers (orientation), l, (sidelength)...
s.source = 'crop.rec'; s.center = 'center';
Here, we set the center of the slice. We can pass a [x,y,z] triplet (like [256,200,100], or just use the code 'center' to put the center of the slice in the center of the tomogram. Now, we indicate the horizontal and vertical lengths of the slice (in pixels):
s.l = [1000,1000];
The actual extent of the slice will get cut if the l that we use is bigger than the size of the tomogram.
The orientation of the slice can be computed through a combination of euler angles [tdrort, tilt, narot], or simply with strings 'x', 'y' and 'z' for orthogonal directions.
s.eulers = 'z';
You can also input euler triplets as value for property eulers. Other properties you can fix are bandpass or thickness.
Now, we actually compute the slice;
s.fetchData();
This will not create any output in the screen. fetchData will just operate the action of visiting the file crop.rec and extracting a numeric matrix that represents the gray intensities of the slice with the indicated parameters. The matrix will be stored inside the s object (as the 'data' property) and will be accessed by the depicting operations to be executed later. General help on this class can be found in
help dpktomo.volume.slices.Slice
The slice depictor object
We first create a figure with and empty axis:
f = figure; haxis = gca();hold on;
Here, f and haxis are handles that will be used later to direct the graphical output to our figure.
Now, we initialize a depiction object associated with the slice s
sz = dpktomo.volume.slices.SliceGraphic(s);
Note that no graphical output has been created yet. We first inform the object sz in which axis it is to be created.
sz.axis.h = haxis;
and then create the slice in the available axis.
sz.create();
If the figure is below other windows in your system you can rise it through
shg;
or
figure(f);
We can change the angle of view with the rotation icon or programmatically:
view([-38,60]);
Placement of templates
Here we will place copies of an FHV crown in the positions and orientations given by a table. Here, the density map representing the template needs first to be converted into an isosurface, which will be represented by a triangulation.
Creating a mask
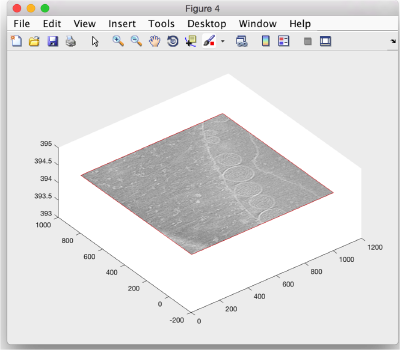
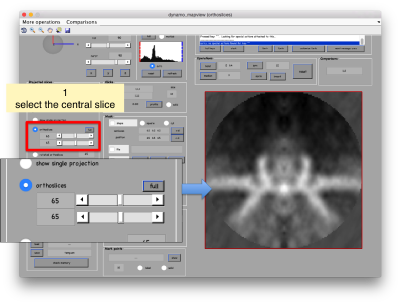
We first want to crop the available average inside a mask, to get rid of the membrane surrounding the crown. For this we first show the template inside mapview
dmapview averagedLocalRefinement.em
We can apply a 'c12' symmetrization on the template to get better graphical depiction.
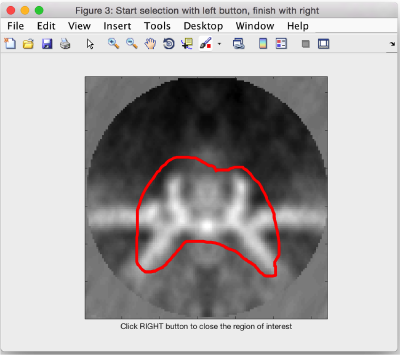
Now, we can select the area of interest by moving to the central section
If you click on shift + S you will get a popup window where you can draw an area of interest. Dynamo will create a revolution solid by rotating the mask that your depict in 2d (on the xz plane) about the z axis. Use the main click to start drawing and the auxiliary click where you are done.
We read the created mask from the file where Dynamo creates it by default
maskRevolution = dynamo_read('temp_drawn_revolution_mask.em');
and apply it onto our template. We apply the 12-fold symmetrization on the same operation.
template = dread('averagedLocalRefinement.em');
final = dsym(template,'c12').*maskRevolution;
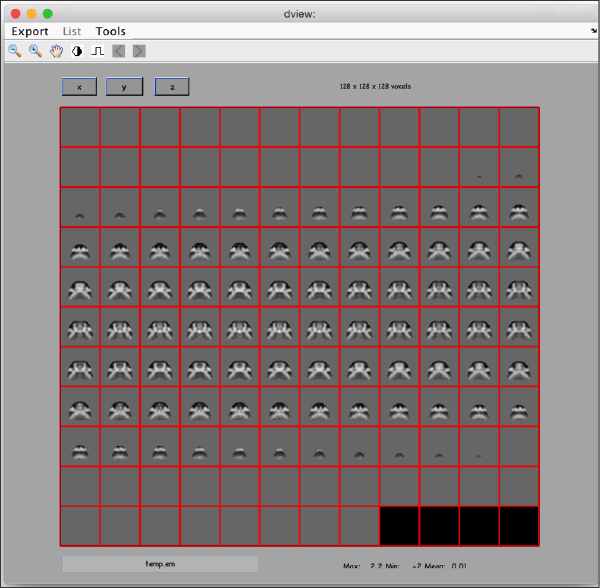
Here the A .* B notation indicates the pixelwise multiplication of two volumes. We can now write the result into a file
dwrite(final,'placedTemplate.em');
and visualize the result:
dview placedTemplate.em
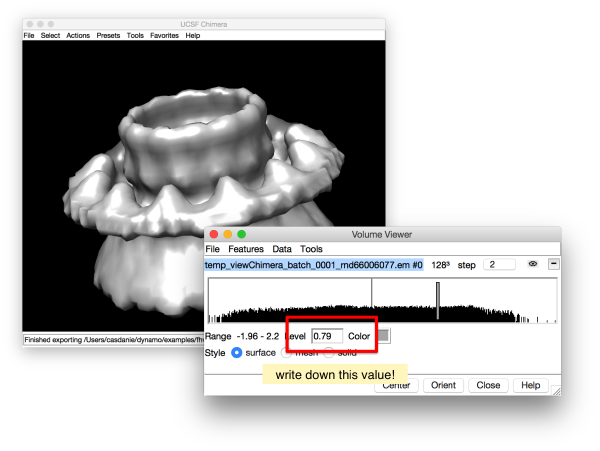
Checking the isolevel in Chimera
You can check the appropriate isolevel using Chimera UCSF, assuming it is activated in your session.
.
Creating a Dynamo triangulation for the template
Ideally, we would like to export the triangulation created in Chimera into Dynamo directly (using the Export as STL file in the Export scene menu of Chimera). However, you have probably moved and rotated the object in Chimera in order to visualize it more clearly. Thus, we will just use the isolevel computed by Chimera and recreate the isosurface inside Dynamo:
dt = dynamo_isosurface(final,'isolevel',0.79,'real_isolevel',true,'-show',false);
Here, the output dt is a Dynamo object that manages isosurfaces. In order to see the isosurface that we just created, we open a new figure:
f2 = figure();
and use the trisurf command of matlab to open the matlab triangulation contained in the property tr.
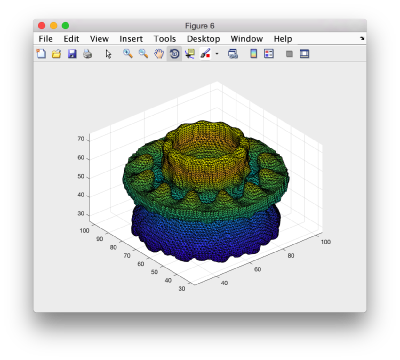
trisurf(dt.tr);axis equal ;
Creating a global triangulation
we recover our table with locations 'and alignment parameters
t = dread('alignmentLocalRefinement.tbl');
and create a triangulation object that merges the result of copying, relocating and rotating the isosurface of one template on all positions of the table:
tAll = dpktbl.triangulation.place(t,dt.tr,'rc',64.5);
Here, 64.6 indicates the position of the rotation center. Note that this does not create a graphical output. tAll is just a triangulation object, which we can depict in our figure t (where we had depicted the slide of the tomogram).
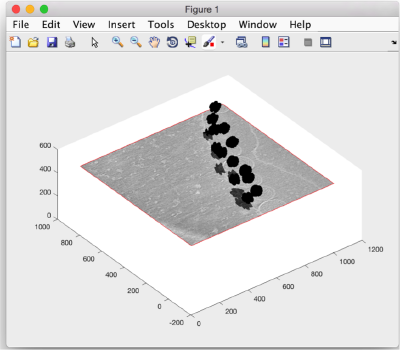
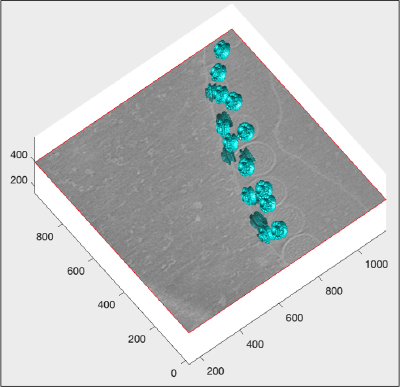
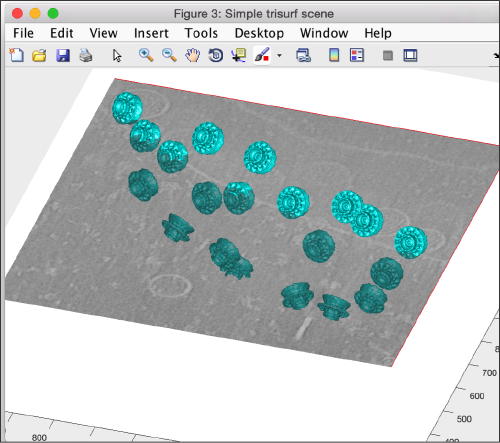
figure(f); hTriangulation = trisurf(tAll); shg;
The created figure looks rather disappointing: we have to adjust the default matlab settings for representation of triangulations. First we ask for depicting only the faces, not the edges:
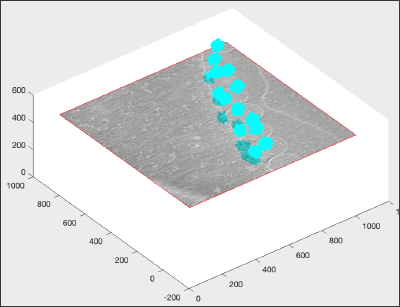
hTriangulation.FaceColor= 'c'; hTriangulation.LineStyle = 'none'; shg;
The object is indeed cyan, but we don't see any details, as we haven't defined any shading:
axis equal; f.Name = 'Simple trisurf scene'; % just m the exploration mbgraph.cursors.setMouse3d([]); shg shading(haxis,'faceted'); l = lightangle(-45,30); shg
Now we see details, but they are overall defined in a grey scale. We need to simulate in Matlab the coexistence of two colormaps in a figure (a feature missing in the native software).
ocm = dynamo_colormap(); shg
Now we repaint the triangulation to cyan.
hTriangulation.FaceColor= 'c';
Moving the slice
If you want to change an existing slice on an already created scene, you need to change some settings.
s.refresher.dataUpdatesAfterGeometryChanges(); sz.surface.autoUpdate();
After them, any change in thickness, band,center,l,eulers will automatically refresh the appearance of the slice, For instance you can shift it upwards through:
s.shift([0,0,100]]);
which is equivalent to
s.center = s.center+[0,0,100];
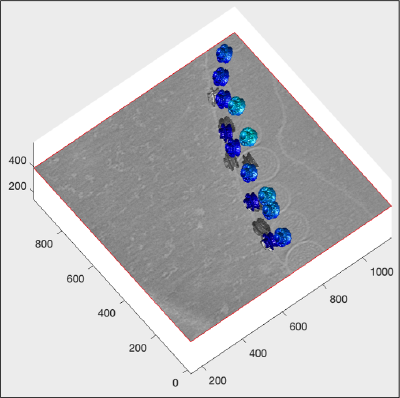
Adding a membrane triangulation
We make sure that we send the graphical output to the correct figure, using the handle we defined previously:
axis(haxis);
We recover our membrane model:
m = dread('membraneModel.omd');
and extract the triangulation hidden inside it (mesh.tr property)
hMem =trisurf(m.mesh.tr);
We may want to adjust the appearance a little, for instance the transparence:
hMem.FaceAlpha = 0.3;